Evaluering av strategiske allokeringsbeslutninger: Regionfordelingen i SPU
Mange investorer velger å delegere forvaltningen av formuen sin til en forvaltningsbedrift. For eksempel har Finansdepartementet delegert gjennomføringen av forvaltningen av SPU («Oljefondet») til Norges Bank. Avkastning og risiko bestemmes da dels av de langsiktige strategiske valgene som oppdragsgiver har tatt og dels av de taktiske avvikene som forvalteren velger å ta. I denne artikkelen presenterer vi et strukturelt rammeverk for å evaluere strategiske valg og gi estimater på verdiskapingen ved disse valgene. Vi anvender dette på en beslutning i 2012 om hvordan aksjeporteføljen til SPU skulle fordeles på tvers av fire globale regioner.
Evaluering av strategiske allokeringsbeslutninger: Regionfordelingen i SPU1
Innledning
Statens pensjonsfond utland (SPU eller «Oljefondet») fikk en ny referanseindeks i 2012. Denne referanseindeksen anga blant annet hvordan SPUs aksjeportefølje skulle fordeles mellom fire globale regioner. NBIM (2020a) viser en figur som indikerer at beslutningen om regionfordelingen av fondets aksjeverdier medførte et tap på nesten 600 milliarder kroner mellom 2012 og 2020.2Dette beløpet er i størrelsesorden 20 prosent av fastland-Norges årlige BNP, seks prosent av fondet eller to års overføringer fra fondet til statsbudsjettet.
I denne artikkelen vurderer vi beslutningen som ble tatt i 2012 om de relative vektene til de fire regionene. På beslutningstidspunktet var utfallet som senere fulgte, bare ett av, i prinsippet, uendelig mange mulige utfall. Det realiserte tapet som NBIM (2020a) viste, er derfor i seg selv et uegnet mål på hvor god eller dårlig denne beslutningen var. Vi gir i stedet et strukturelt estimat på hva den finansielle verdiskapingen ved denne beslutningen var ut fra informasjonsgrunnlaget som dengang var tilgjengelig. Artikkelen er også et metodologisk bidrag til hvordan analysere og estimere verdiskapingen ved strategiske allokeringer generelt, herunder de strategiske valgene som avgjør avkastningen og risikoen ved SPU.
Institusjonelt rammeverk for forvaltningen av SPU
Mandatet fra Finansdepartementet til Norges Bank inneholder en strategisk referanseindeks og tilhørende rammer for forvaltningen. Aksjer utgjør 70 prosent og obligasjoner 30 prosent. Den strategiske referanseindeksen består av separate indekser for aksjer og obligasjoner. Referanseindeksene tar utgangspunkt i indekser fra eksterne leverandører og definerer videre forhold som hvordan aksjene skal være fordelt mellom forskjellige regioner, hvordan obligasjonsporteføljen skal være fordelt mellom statsobligasjoner og selskapsobligasjoner, hvor risikable selskapsobligasjoner kan være, hvor lang løpetid obligasjonene i snitt bør ha, med mer. Finansdepartementets mandat til Norges Bank gir banken en begrenset ramme for avvik fra referanseindeksen slik at Norges Bank kan implementere den på en kostnadseffektiv måte og tjene penger på forvaltningsaktiviteter hvor det er stordriftsfordeler.
Den strategiske referanseindeksen refereres gjerne til som den «strategiske aktivaallokeringen». Eventuelle avvik som forvalter, i dette tilfellet Norges Bank, velger å ta, refereres til som den «taktiske aktivaallokeringen». Avkastning og risiko for SPU bestemmes nesten utelukkende av den strategiske aktivaallokeringen, med andre ord beslutningene som Finansdepartementet tar på vegne av eierne og som reflekteres i referanseindeksen (se for eksempel Dahlquist og Ødegaard, 2018).
Referanseindeksen for aksjer fikk nye regionvekter i 2012. Vektene angir hvordan fondets aksjebeholdning skal fordeles over henholdsvis utviklede markeder i Europa, Nord-Amerika, Asia/Oseania, og i fremvoksende markeder. Det viktigste ved beslutningen i 2012 var at regionvektene la betydelig større vekt på investeringer i Europa enn markedsvekter skulle tilsi og betydelig mindre vekt på investeringer i Nord-Amerika. Vektene for de fire regionene lå fast inntil de ble revidert i 2020, og vi fokuserer derfor i hovedsak på tidsperioden fra 2012 til 2020 i denne artikkelen.
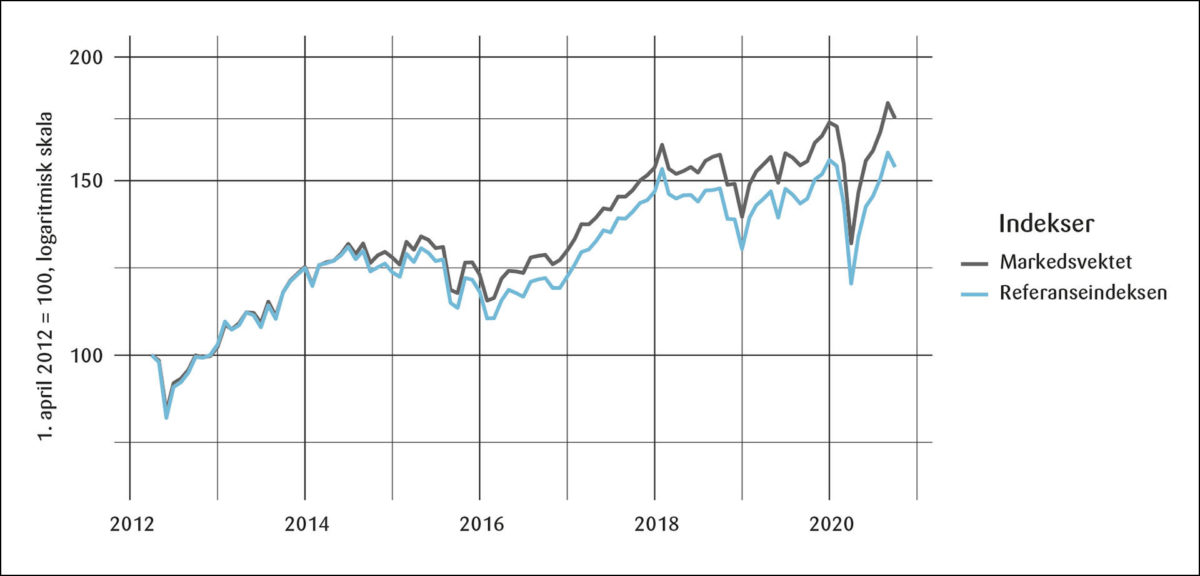
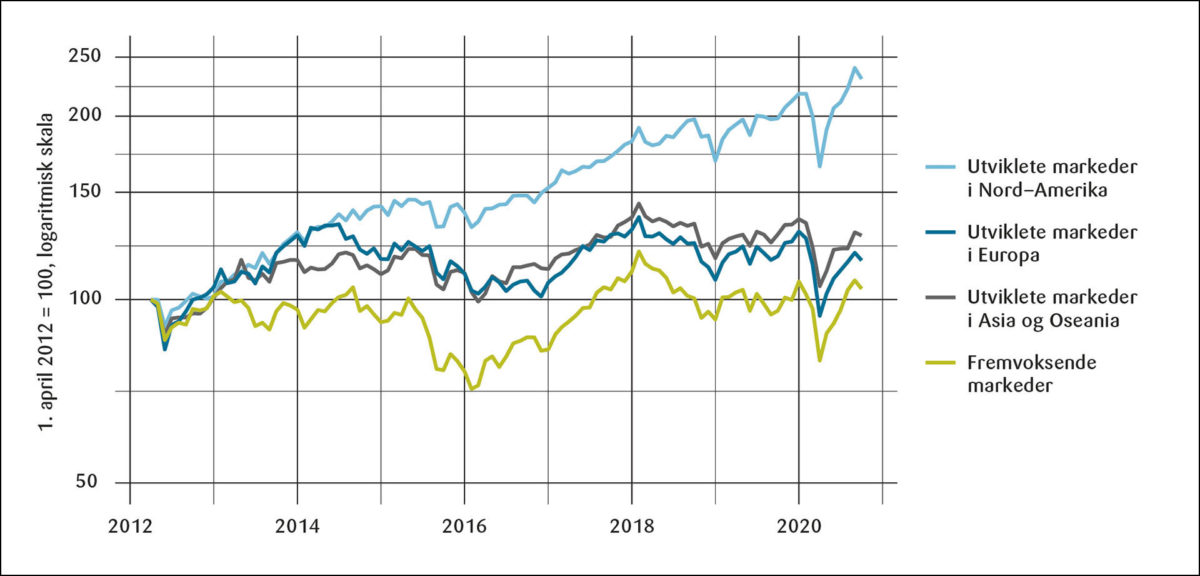
Markedsutvikling 2012–2020
Figur 1 viser utviklingen i SPUs referanseindeks og en indeks basert på markedsverdivekter mellom 1. april 2012 og 1. oktober 2020. Som vi ser har avkastningen i den markedsverdivektede indeksen vært betydelig høyere enn i referanseindeksen i denne perioden. Grunnen til denne forskjellen vises i Figur 2. Den regionen med klart høyest avkastning mellom våren 2012 og høsten 2020 var Nord-Amerika som hadde lavere vekt i referanseindeksen til SPU enn det markedsverdivekter ville ha tilsagt. Avkastningen i utviklede markeder i Europa, som hadde høyere vekt, var litt høyere enn i fremvoksende markeder, men dårligere enn i utviklede markeder i Asia og Oseania.
Et rammeverk for å evaluere strategiske valg
Modellene for å evaluere taktiske aktivaallokeringer har etter hvert blitt sofistikerte. Disse modellene analyserer om fondsforvaltere har skapt eller ødelagt verdier ved de valgte avvikene fra sine referanseindekser. Siden fondsforvaltere i prinsippet har mulighet til å endre sammensetningen av porteføljen flere ganger hver dag, vil det være et stort antall beslutninger som blir evaluert. Det er derfor mulig å bruke statistiske metoder. For slike statistiske sammenligninger benyttes gjerne en én-, tre-, fire- eller fem-faktor modell (se for eksempel Jensen, 1968; Fama og French, 1993; Carhart, 1997; Fama og French, 2015). Selv om det er heftet statistiske og konseptuelle utfordringer ved å evaluere forvaltere på denne måten, og det gjøres stadig viktige forskningsbidrag for å forbedre disse metodene, så kan dette problemet karakteriseres som vel forstått.
For eieren av et fond eller en portefølje er generelt valget av strategisk aktivaallokering og referanseindeks langt viktigere for avkastning og risiko enn forvalters taktiske avvik fra indeksen. Til tross for dette, eksisterer det oss bekjent knapt noen litteratur om evaluering av langsiktige strategiske valg, mens det finnes en omfattende litteratur om evaluering av taktiske avvik.
Siden det er snakk om én eller et lite antall strategiske beslutninger, er det ikke mulig å anvende de samme statistiske verktøyene som benyttes for å evaluere porteføljeforvaltere. Det er i stedet nødvendig å benytte en strukturell tilnærming slik vi gjør i rammeverket som presenteres i denne artikkelen.
Den metodologiske tilnærmingen vår har to hoveddeler. I den første delen beskriver vi et strukturelt rammeverk for å estimere gevinsten (eller kostnaden) av én investors strategiske aktivaallokering. Vårt estimat på den finansielle verdiskapingen ved et porteføljevalg er basert på hva denne individuelle investoren ville kreve i betaling (eller vært villig til å betale) for å være indifferent mellom to risikable porteføljer. Dette tilsvarer den kompenserende variasjonen som er lik differansen mellom sikkerhetsekvivalentene for de to porteføljene.
For å gi kvantitative estimater for gevinsten (eller kostnaden) av den individuelle investorens beslutning, er det nødvendig å ha markedets forventete avkastning og risiko for alle porteføljens bestandeler. I den andre delen introduserer vi en metode for å estimere forventete avkastninger for hele settet av mulige aktiva på beslutningstidspunktet. I motsetning til den første delen som analyserte valget til én individuell investor så tar estimatene i den andre delen utgangspunkt i valgene til gjennomsnittsinvestoren og med det markedsklarerering.
Nært relatert til at ett utfall fra en stokastisk fordeling ikke gir grunnlag for å fastslå om én beslutning var god eller dårlig, er spørsmålet om hvor sannsynlig det ene realiserte utfallet var på beslutningstidspunktet. Vi gir derfor også et strukturelt estimat for sannsynligheten for et så stort avvik mellom referanseindeksen og markedsporteføljen som ble utfallet i perioden vi studerer. Estimatet indikerer at sannsynligheten var liten, men ikke neglisjerbar.
Det analytiske rammeverket vi presenterer er generelt og kan benyttes for å evaluere andre strategiske allokeringsbeslutninger og valg som inngår i referanseindekser. Elementene i tilnærmingen vår har tidligere vært presentert i publiserte artikler og lærebøker. Bidraget vårt er primært knyttet til spørsmålet vi stiller og måten disse elementene kombineres for å gi strukturelle estimat på verdiskapingen ved strategiske allokeringsbeslutninger.
Tabell 1: Regionfordeling i markedsindekser og SPUs justeringsfaktorer.v
| Utviklede markeder i Europa | Utviklede markeder i Nord-Amerika | Øvrige utviklede markeder | Fremvoksende markeder | |
|---|---|---|---|---|
| 1. april 2012 | ||||
| Markedsvekter | 0,23 | 0,50 | 0,15 | 0,12 |
| Justeringsfaktorer | 2,5 | 1,0 | 1,5 | 1,5 |
| Justerte vekter | 0,39 | 0,34 | 0,15 | 0,12 |
| 1. oktober 2020 | ||||
| Markedsvekter | 0,15 | 0,66 | 0,11 | 0,07 |
| Justeringsfaktorer | 2,0 | 1,15 | 1,5 | 1,5 |
| Justerte vekter | 0,23 | 0,57 | 0,12 | 0,08 |
Den geografiske fordelingen av aksjebeholdningen i SPU
Frem til 2012 spesifiserte referanseindeksen for SPU at regionvektene for aksjer skulle være konstante. Til enhver tid skulle 50 prosent av markedsverdien av aksjeporteføljen være børsnotert i Vest-Europa, 35 prosent i Nord-Amerika og 15 prosent i Asia og Oseania.
I mars 2012 ble det foreslått at regionfordelingen i stedet burde variere med utviklingen i samlete markedsverdier. Den nye fordelingen delte aksjemarkedet inn i fire regioner – utviklede markeder i Europa, utviklede markeder i Nord-Amerika, øvrige utviklede markeder og fremvoksende markeder – og vektingen i disse regionene skulle ta utgangspunkt i de forskjellige regionenes andel av det samlede aksjemarkedet. Det vil si, fordelingen skulle ta utgangspunkt i markedsvektene. Regionfordelingen ble imidlertid ikke fastsatt utelukkende basert på markedsvektene. Regionene ble i tillegg tildelt justeringsfaktorer som sørget for at overvekten i europeiske og undervekten i amerikanske aksjer fra de tidligere faste vektene ble videreført.
De nye vektene på de fire regionene som følger av disse beslutningene, får vi ved å gange markedsvekten for hver region med regionens justeringsfaktor og så normalisere dette produktet. Normaliseringen sørger for at de justerte vektene summerer til 1. For eksempel gis den justerte vekten for Utviklede markeder i Europa av følgende uttrykk:
Med de justerte vektene fra 2012 ble det dermed fortsatt et betydelig avvik fra markedsvekter i fondets referanseindeks. Som en illustrasjon av dette eide SPU ved utgangen av 2020 i gjennomsnitt 2,5 prosent av de omsettbare aksjene i hvert børsnoterte selskap i Europa, mens fondet eide 1,0 prosent av de omsettbare aksjene i hvert børsnoterte selskap i Nord-Amerika.3
I Meld. St. 32 (2019–2020) foreslo Finansdepartementet å endre justeringsfaktorene ved å justere andelen investert i Europa noe ned og andelen i Nord-Amerika noe opp relativt til vektene fra 2012. Dette vil si at Finansdepartementet la opp til at vektene i SPUs referanseindeks skulle nærme seg markedsvektene. Tabell 1 viser markedsvektene, justeringsfaktorene og de justerte vektene i referanseindeksen basert på beslutningen fra april 2012 og de nye justeringsfaktorene og vektene i referanseindeksen i oktober 2020. Tabellen viser at Finansdepartementets forslag fortsatt innebærer et betydelig avvik mellom markedsvektene og referanseindeksen. Forslaget ble vedtatt i Stortinget i desember 2020.
Begrunnelse
Ifølge Finansdepartementet har den høye andelen europeiske aksjer i SPUs referanseindeks vært knyttet til valutarisiko forbundet med importen i Norge. Departementet skriver: «Forskjeller i sammensetningen av konsum av internasjonale varer og tjenester gir også investorene ulik valutarisiko. Dersom valutasammensetningen av aksjeinvesteringene benyttes til å motvirke slik valutarisiko, vil også den geografiske sammensetningen av aksjeinvesteringene kunne variere hos investorer».4,5 Det var imidlertid aldri aktuelt å la vektene utelukkende avgjøres av Norges import da dette for eksempel ville føre til en betydelig overvekt i svenske aksjer i porteføljen.
Historisk har referanseindeksen for aksjer hatt en høyere vekt for europeiske aksjer enn det markedsverdivekter skulle ha tilsagt. Innen hver region var det markedsvekter som ble valgt i sammensetningen av aksjeinvesteringene i den regionen. Men i vektingen av regionene ble valget av vekter for aksjeinvesteringene påvirket av hensyn til obligasjonsporteføljen. I Norges Banks brev til Finansdepartementet 22. august 1997 skrev Norges Bank at den «regionale fordelingen bør være lik for aksjer og obligasjoner» og at markedsvekter ikke er hensiktsmessig for obligasjonsporteføljen. Derfor anbefalte Norges Bank at det legges mest vekt på BNP-vekter, men også tas hensyn til Norges importmønster.6
Begrunnelsen for regionvektene har ikke åpenbar støtte i lærebøker og forskningslitteratur. I fravær av dokumenterte egenskaper ved andre eiendeler eller utestående forpliktelser vil standard lærebøker, som for eksempel Cochrane (2005), Back (2017) og Campbell (2018), peke på den markedsverdivektede porteføljen som den ex ante optimale. I følge de samme lærebøkene vil hensyn til de stokastiske egenskapene ved øvrig formue eller utestående forpliktelser kunne gjøre det hensiktsmessig å avvike fra markedsverdivekter i den finansielle formuen. Det virker imidlertid ikke som beslutningen om å eie en større andel europeiske aksjer enn det markedsverdivekter har tilsagt, fulgte av et porteføljeoptimeringsproblem som tok hensyn til Norges ikke-finansielle formue eller utestående forpliktelser.
Realisert avkastning og variasjon 2012–2020
For å illustrere viktigheten av valgene som inngår i referanseindeksen generelt, og valget av regionfordeling i særdeleshet, viser vi i dette avsnittet den realiserte avkastningen for de fire regionene mellom 2012 og 2020. Vi sammenligner de valgte regionvektene i referanseindeksen med regionvekter som hadde vært sammenfallende med relative markedsverdivekter. Vi benytter markedsvekter som sammenligningsgrunnlag siden det er hva lærebøker peker på som det naturlige utgangspunktet for porteføljevalg.
På beslutningstidspunktet kunne man selvfølgelig ikke vite hva denne realiserte avkastningen ville bli, men det er likevel interessant å estimere tapet eller gevinsten målt i kroner som fulgte av valget som ble tatt i 2012. Derfor utdyper vi her resultatene i Figur 1 og 2 og presenterer en ex-post sammenligning av referanseindeksen og markedsindeksen basert på den realiserte utviklingen fra 2012 til 2020. En slik sammenligning er også en test på om vi med vår håndtering av endringer i valutakurs, aksjeandel og innflyt kommer til omtrent samme svar som vist i NBIM (2020a).
Realiserte avkastningsforskjeller målt ved Sharpe-rater
For å kunne sammenligne to porteføljer som kan være forskjellige i både avkastning og risiko, trenger vi et kriterium som fanger opp avveiningen mellom disse hensynene. Kriteriet vi benytter er Sharpe-raten, og for en gitt portefølje defineres denne som følger:
(1)
Notasjonen vi benytter er at Rp er realisert avkastning på en portefølje, Rf er den risikofrie renten, og Rp– er den realiserte avkastningen utover den risikofrie renten. Til slutt er σp det realiserte standardavviket på porteføljen.
Sharpe-raten slik den fremstår i ligning (1) kan benyttes i en ex-post sammenligning av forskjellige porteføljer hvor man ser bakover i tid og dermed vet både realisert avkastning og variasjon. Dette gir en bedre ex-post evaluering enn kun å se på de realiserte avkastningene slik som i Figur 1 fordi det er mulig at en lavere realisert avkastning sammenfaller med lavere variasjon i avkastningen.
Vi ønsker å sammenligne referanseindeksen og markedsindeksen basert på realiserte avkastninger, realiserte standardavvik og realiserte, annualiserte Sharpe-rater. For å beregne disse ratene konstruerer vi de to porteføljene 1. april 2012 basert på markedsvektene og på referanseindeksens justerte vekter for de fire regionene vist i Tabell 1. Deretter beregner vi utviklingen i porteføljene frem til 1. oktober 2020 basert på utviklingen i aksjeindeksene i de fire regionene.
Tabell 2: Realisert avkastning og variasjon (prosent), månedlig, 1. april 2012 til 1. oktober 2020
| MSCI indeks | Europa | Nord-Amerika | Øvrige utviklede markeder | Fremvoksende markeder |
|---|---|---|---|---|
| Avkastning | 0,15 | 0,82 | 0,24 | 0,04 |
| Standardavvik | 4,56 | 4,28 | 3,93 | 4,82 |
Tabell 2 viser regionenes gjennomsnittlige månedlig avkastning og standardavvik.7 Vi ser at Nord-Amerika skiller seg ut med høyest avkastning. Lavest variasjon har indeksen for øvrige utviklede markeder. Det kan innebære diversifiseringsgevinster å inkludere alle indeksene i porteføljene, og diversifiseringsgevinstene vil avhenge av korrelasjonen mellom avkastningene i alle regionene som ikke vises av plasshensyn. Realiserte annualiserte tall for de to porteføljene vises i Tabell 3.8
Tabell 3: Realiserte tall, annualisert, 1. april 2012 til 1. oktober 2020
| Rp- (prosent) | Standardavvik (prosent) | Sharpe-rate (ex-post) | |
|---|---|---|---|
| Markedsporteføljen | 6,0 | 14,3 | 0,42 |
| Referanseindeksen | 4,6 | 14,4 | 0,32 |
Beregningene gir et klart resultat: Avkastningen i markedsporteføljen var 1,4 prosent høyere per år, og risikoen i de to porteføljene var tilnærmet lik. Dermed ville investeringer basert på markedsvektene gi en betydelig høyere avkastning i perioden uten at det innebar noe høyere risiko. Dette reflekteres i den realiserte Sharpe-raten som indikerer at markedsporteføljen ga en betydelig bedre avveining mellom avkastning og risiko enn SPUs referanseindeks.
Realiserte avkastningsforskjeller målt i kroner
Hva blir så betydningen av denne forskjellen i avkastning i norske kroner? Det er ikke helt enkelt å gjøre en nøyaktig beregning av dette. Viktigheten av avkastningen på aksjeinvesteringene for SPUs samlede avkastning avhenger av fondets aksjeandel som i 2017 ble endret fra 60 til 70 prosent etter forslag fra Mork-utvalget. I tillegg har fondet vokst i perioden på grunn av tilførsel av oljeinntekter, og fondsverdien målt i norske kroner har økt på grunn av svekkelser i kronekursen. Uklarhet om hvordan rebalanseringsregelen har blitt implementert i praksis gjør det også vanskeligere å finne et presist estimat på differanseavkastningen målt i norske kroner. Vi kan imidlertid beregne en nedre og en øvre grense for betydningen av den valgte regionfordelingen ved å ta utgangspunkt i fondets størrelse ved inngangen av 2012 og ved utgangen av 2020.
Ved inngangen av 2012 var verdien av fondet 3.312 milliarder kroner.9 Så antar vi at aksjeandelen lå fast i perioden på 60 prosent, og vi ignorerer økninger i fondets verdi som skyldes både tilførsel av oljeinntekter og svekkelse av kronekursen. Vi gjennomfører årlig rebalansering tilbake til 60 prosent aksjeandel. Siden den i stor grad kanselleres ut, har vår approksimasjon for porteføljen av renteinstrumenter og unotert eiendom liten betydning. For enkelhets skyld antar vi at avkastningen på denne delen av porteføljen er lik den risikofrie renten.
Basert på disse antagelsene får vi at investering av midlene med 60 prosent i markedsporteføljen i en periode på 8,5 år ville vokst til 4.735 milliarder. En investering hvor aksjedelen i stedet fulgte referanseindeksen ville vokst til 4.420 milliarder kroner. Differansen på 315 milliarder kroner utgjør dermed en nedre grense for den estimerte realiserte avkastningsforskjellen mellom markedsporteføljen og referanseindeksen i den valgte tidsperioden.
Vi kan også beregne en øvre grense for betydningen av dette porteføljevalget ved å ta utgangspunkt i fondets størrelse ved utgangen av 2020 som var 10.914 milliarder kroner. Så antar vi at dette ble oppnådd med en aksjeandel på 70 prosent i hele perioden, og igjen ignorerer vi at en betydelig del av denne verdien skyldes tilførsel av oljeinntekter og svekkelse av kronekursen. Dermed antar vi at dette beløpet ble oppnådd kun ved investering av 70 prosent i referanseindeksen og 30 prosent i den risikofrie renten over en periode på 8,5 år. Da ville utgangspunktet ha vært et fond på 7.874 milliarder kroner.
Hvis dette fondet i stedet hadde blitt investert med 70 prosent i markedsporteføljen og resten i den risikofrie renten, så ville fondets størrelse etter 8,5 år være på 11.822 milliarder kroner. Differansen på 908 milliarder kroner utgjør dermed en øvre grense for et estimat på kostnaden ved å avvike fra markedsporteføljen med den valgte regionfordelingen over denne perioden.
Et mer nøyaktig anslag på denne kostnaden er vanskelig å komme frem til. For å gjøre det måtte vi som nevnt ha høyfrekvente tall på tilførsel av oljeinntekter, endringer i kronekurs, og detaljert kunnskap om implementeringen av overgangen fra en aksjeandel på 60 prosent til en andel på 70 prosent og om implementeringen av rebalanseringsregelen.
Gjennomsnittet av våre estimater for en øvre og nedre grense for denne kostnaden er på 611,5 milliarder kroner. Dette er ikke et nøyaktig anslag på betydningen av den valgte regionfordelingen, men beregningene indikerer at forskjellene i avkastning mellom markedsindeksen og referanseindeksen som vises i Figur 1, utgjør en forskjell i realisert avkastning på flere hundre milliarder kroner. Dette understreker viktigheten av sammensetningen av SPUs referanseindeks.
Rammeverk del 1: Evaluering av en allokeringsbeslutning
I denne delen presenterer vi et kriterium for å evaluere en strategisk allokeringsbeslutning for en individuell investor. Dette kriteriet er basert på hva investoren ville vært villig til å betale (eller kreve i sikker betaling) for å være indifferent mellom to risikable porteføljer. I neste del presenterer vi en metode for å kvantifisere dette kriteriet og gi et estimat på verdiskapingen eller tapet ved denne beslutningen.
Den finansielle verdiskapingen av en allokeringsbeslutning må være relatert til kompensasjonen som ville gjort en individuell investor indifferent mellom to porteføljer med forskjellig forventet avkastning og risiko. Dette kan sammenlignes med begrepet «sikkerhetsekvivalent» fra teori om beslutninger under usikkerhet. Det er det sikre beløpet som ville gjort investoren indifferent mellom dette beløpet og et risikabelt lotteri. Begrepet er nært relatert til «kompenserende variasjon» og «ekvivalent variasjon» fra generell økonomisk teori og velferdsanalyse.
I vårt tilfelle vil vi imidlertid sammenligne to risikable porteføljer av vilkårlig størrelse. I stedet for å beregne et sikkerhetsekvivalent beløp beregner vi en tilsvarende ekvivalent risikofri avkastning for en risikabel portefølje som ville gjort investoren indifferent mellom å holde den risikable porteføljen eller å få den risikofrie avkastningen. Verdiskapningen ved å velge en risikabel portefølje fremfor en annen gis da av differansen mellom de to tilsvarende risikofrie avkastningene.
Investors preferanser vil være avgjørende for hvilken risikofri avkastning som gjør henne indifferent mellom denne og en risikabel portefølje-avkastning. Investorens indifferenskurve definerer vi som følger:
(2)
hvor U¯ er et gitt nivå for investorens nytte, og funksjonen f(σ) gir den forventete avkastningen E[R] som en portefølje med et standardavvik på σ må ha for at investoren skal oppnå en nytte lik U¯. Funksjonen viser da hvor mye forventet avkastning må endres for å holde investoren indifferent når forventet standardavvik endres.
Med et uttrykk for investorens indifferenskurve, kan vi regne ut den nytten investoren får av å holde en risikabel portefølje. Bruker vi dette nivået på nytten for U¯ i ligning (2), kan vi også beregne f(0). Det gir den avkastningen en portefølje med et standardavvik på 0 må ha for at investoren skal oppnå samme nytte som ved å holde den risikable porteføljen, det vil si den risikofrie avkastningen som ville gjort investoren indifferent.
Vi er agnostiske til den parametriske formen og krumningen til investorens nyttefunksjon og indifferenskurve. Vi diskuterer derfor henholdsvis en førsteordens og en andreordens tilnærming av en, i prinsippet, vilkårlig indifferenskurve rundt det teoretisk optimale porteføljevalget. For det optimale porteføljevalget kan vi utlede stigningstallet til indifferenskurven. Det er med andre ord mulig å utlede to egenskaper ved indifferenskurven til investoren uten å gjøre noen antagelse om formen på nyttefunksjonen: nivå og stigningstall i ett punkt.
Sammenligningsportefølje
Porteføljen som vi sammenligner SPUs referanseindeks med, burde være den teoretisk optimale porteføljen på beslutningstidspunktet. I denne artikkelen velger vi å anta at det optimale porteføljevalget i 2012 ville vært en portefølje hvor regionvektene sammenfalt med markedsverdivekter. Markedsvekter er, som skrevet, et vanlig utgangspunkt i porteføljeteori. Dette er for eksempel resultatet i kapitalverdimodellen presentert i Sharpe (1964), Lintner (1965) og Mossin (1966), og i en internasjonal versjon av denne i Stulz (1981). I en internasjonal versjon betegnes ofte markedsporteføljen som «verdensporteføljen», og i vårt tilfelle består altså denne av de fire regionene SPU kan investere i.10,11
Spørsmålet er om det er en annen portefølje enn den markedsvektede verdensporteføljen som ville være den optimale å sammenligne med? En slik portefølje kunne for eksempel tatt hensyn til Norges ikke-finansielle formue i form av forventete fremtidige olje- og gassintekter og dermed gitt en annen optimal regionfordeling. Det er utenfor rekkevidden til denne artikkelen å gjennomføre en slik analyse, men rammeverket som presenteres her kan benyttes til å vurdere avviket mellom referanseindeksen og en eventuell annen optimal regionfordeling.
En førsteordens tilnærming til indifferenskurven
Vi er som skrevet agnostiske med hensyn til både den parametriske formen og til parameterne som inngår i nyttefunksjonen. Vi vil derfor heller vurdere Taylor-tilnærminger rundt det teoretisk optimale porteføljevalget. Om vi kjenner den teoretisk optimale porteføljen og kjenner stigningstallet for tangenten for investorens indifferenskurve, så kan vi presist identifisere en førsteordens tilnærming.
En førsteordens tilnærming til indifferenskurven i ligning (2) rundt den optimale porteføljen gis av følgende ligning:
(3)
Når vi tar utgangspunkt i at den markedsvektede indeksen var det optimale valget av portefølje for investoren, så tar vi tilnærmingen rundt punktet for markedsindeksen. Det vil si punktet (hvor ). Grafisk ville dette bety å tegne indifferenskurven gjennom punktet for markedsindeksen og å trekke en rett linje tangent til denne kurven som også går igjennom dette punktet. Kapitalmarkedslinjen med stigningstall lik markedsindeksens Sharpe-rate er også tangent til indifferenskurven ved dette punktet, så det følger at førsteordenstilnærmingen til indifferenskurven må ha det samme stigningstallet. Dermed får vi at .
Vi kan nå benytte førsteordenstilnærmingen til å beregne den risikofrie avkastningen som gjør investoren indifferent mellom denne avkastningen og en risikabel portefølje. Vi referer til denne risikofrie avkastningen som porteføljens «sikkerhetsekvivalent» selv om dette muligens er noe upresist. Sikkerhetsekvivalenten er dermed en portefølje med som gjør investoren indifferent. For markedsporteføljen vil den gis av følgende risikofrie avkastning:
Vi kan også beregne sikkerhetsekvivalenten for SPUs referanseindeks for denne investoren. For å gjøre det flytter vi førsteordenstilnærmingen til investorens indifferenskurve (en linje med stigningstall ) til punktet ( ). Sikkerhetsekvivalenten for SPUs referanseindeks blir da:
Den finansielle verdiskapingen ved allokeringsbeslutningen, målt ved en førsteordens tilnærming, blir da
(4)
hvor tallet 1 i senket skrift på variabelen V indikerer at disse størrelsene er beregnet ved en førsteordens tilnærming. Dermed får vi et mål på kostnaden ved å avvike fra markedsvektene i SPUs referanseindeks.
En andreordens tilnærming til indifferenskurven
Å benytte en førsteordens tilnærming av investorens indifferenskurve er ekvivalent til å anta at investoren har en lineær nyttefunksjon. En åpenbar ulempe ved denne fremgangsmåten er at vi da ignorerer investorens risikoaversjon. Risikoaversjon er et naturlig element å ta hensyn til når det gjelder porteføljevalg som innebærer avveining mellom risiko og forventet avkastning. Derfor ønsker vi et andreordens uttrykk for indifferenskurven som også påvirkes av forskjellige grader av risikoaversjon.
Investorens risikoaversjon er relatert til graden av krumning av hennes nyttefunksjon som vi ikke observerer. Vi må derfor gjøre en antagelse om formen på denne nyttefunksjonen, men vår tilnærming avhenger ikke av hvilken antagelse vi gjør. I teksten velger vi å benytte en nyttefunksjon med konstant relativ risikoaversjon (CRRA, fra forkortelsen av den engelske betegnelsen) som det er vanlig å benytte i makroøkonomiske modeller. I tillegg viser vi i vedlegg A hvordan vår tilnærming påvirkes av å velge en nyttefunksjon med konstant absolutt risikoaversjon (CARA) i stedet.
En CRRA nyttefunksjon over investorens formue («wealth»), gis av uttrykket:
(5)
Hvor gir den konstante relative risikoaversjonen.
Beslutningen vi studerer handler imidlertid om et porteføljevalg, og da ønsker vi å formulere investorens problem ut i fra porteføljens avkastning. En investor med en opprinnelig formue på W0 vil ha en formue neste periode som avhenger av porteføljens realiserte avkastning: W = W0 (1 + Rp). En egenskap ved en CRRA nyttefunksjon er at den opprinnelige formuen W0 kun fører til en skalering av nyttefunksjonen og ikke påvirker investorens valg. Dermed kan vi fokusere på porteføljens avkastning og formulere nyttefunksjonen på følgende måte:
(6)
En andreordens tilnærming av denne nyttefunksjonen rundt verdien for forventet avkastning neste periode, 1 + E[Rp], gir uttrykket:
Beslutninger om porteføljer må imidlertid tas under usikkerhet slik at en investor maksimerer forventet nytte. Tar vi forventning av hver side av andreordenstilnærmingen ovenfor får vi:
(7)
fordi forventningsverdien av førsteordensleddet er lik null og fordi forventningsverdien av andreordensleddet inkluderer definisjonen av avkastningens varians (eller standardavvik). Investorens forventete nytte neste periode kan dermed uttrykkes som en funksjon av forventet avkastning og standardavviket på investorens portefølje (se for eksempel Markowitz, 2014).
Vi har nå et andreordensuttrykk for nyttefunksjonen. Fordi vi også her antar at den markedsvektede indeksen er den teoretisk optimale porteføljen vi vil sammenligne med, vil vi igjen karakterisere investorens indifferenskurve gjennom dette punktet. Denne indifferenskurven gis av alle punktene som gir samme forventete nytte som det markedsporteføljen gir. Det vil si alle punktene som gir forventet nytt lik som defineres av:
(8)
Ved å ta det totale differensialet av uttrykket i ligning (8), finner vi den førstederiverte av indifferenskurven (se vedlegg B). Når markedsindeksen antas å være optimal, må det igjen være slik at kapitalmarkedslinjen er tangent til indifferenskurven ved dette punktet. Dermed får vi en ligning vi kan løse for risikoaversjonen som er konsistent med dette optimale valget.
Med en verdi for kan vi igjen beregne sikkerhetsekvivalenter som vi gjorde med en førsteordenstilnærming tidligere. Først kan vi beregne den nytten gjennomsnittsinvestoren oppnår ved å holde SPUs referanseindeks ( ) fra en ligning på samme form som ligning (8). Sikkerhetsekvivalentene for de to porteføljene gis da av punktene hvor indifferenskurvene for markedsporteføljen og SPUs referanseindeks krysser y-aksen og dermed har standardavvik lik null. Uttrykkene for disse sikkerhetsekvivalentene blir dermed:
Den finansielle verdiskapingen målt ved en andreordens tilnærming blir da
(9)
Dermed får vi et mål på kostnaden ved å avvike fra markedsvektene i SPUs refereanseindeks som er en funksjon av investorens risikoaversjon. Som i ligning (4), er dette målet kun basert på informasjon som var tilgjengelig da vektene i referanseindeksen ble valgt.
Verdien for risikoaversjonsparameteret
Dersom vi ønsker å benytte uttrykket i ligning (9) for å sammenligne markedsindeksen og SPUs referanseindeks, så trenger vi også en verdi for γ, den individuelle investorens risikoaversjon. Risikoaversjonen er en viktig størrelse i flere sammenhenger i finansiell økonomi. Det er ikke trivielt å kalibrere denne parameteren, og forskjellige tilnærminger har en tendens til å gi svært forskjellige resultater. Vi benytter derfor to forskjellige tilnærminger for å sette en verdi for γ.
Den første tilnærmingen tar utgangspunkt i en modell hvor nivåene på risikofri rente og markedets risikopremie er eksogent gitt. Spørsmålet som studeres er hvordan en investor skal allokere formuen sin mellom forskjellige risikable finansielle instrumenter. Basert på tall for forventete avkastninger og risiko fastsetter vi da risikoaversjonen fra antagelsen om at investorens optimale valg er å kun investere i markedsporteføljen. Ved å fastsette risikoaversjonen med denne tilnærmingen vil man generelt få en relativt lav verdi for risikoaversjonsparameteret.
Den andre tilnærmingen er å vise til litteraturen innen finansiell økonomi som forsøker å redegjøre for nivåene på risikofri rente og forventet avkastning på risikable finansielle instrumenter ved å knytte disse til makroøkonomiske størrelser som konsum og produksjon. Innenfor denne litteraturen er et viktig spørsmål hva som forklarer størrelsen på risikopremien som investorer har fått ved å investere i aksjer. Historisk har denne risikopremien vært betydelig. Den eksakte verdien for γ som man ender opp med vil variere med hvilket marked og hvilken tidsperiode som studeres, men denne tilnærmingen vil typisk gi en høy verdi for risikoaversjonsparameteret.
For utdyping av disse tilnærmingene og avveiingene, vennligst se vedlegg C.
Rammeverk del 2: Forventet risiko og avkastning på beslutningstidspunktet
For å benytte uttrykkene i ligning (4) og ligning (9) og gi kvantitative anslag på den finansielle verdiskapingen av beslutningen må vi tallfeste en del størrelser på beslutningstidspunktet. Det vi trenger er forventet avkastning, varians og kovarians for elementene i porteføljene som skal sammenlignes (i tillegg til risikoaversjonen som vi diskuterte i underkapittelet Verdien for risikoaversjonsparameteret). Utfordringen er at ingen av disse forventningsverdiene er direkte observerbare.
For å estimere disse forventningsverdiene tar vi utgangspunkt i valgene som gjennomsnittsinvestoren i markedet har tatt, to ukontroversielle antagelser og ett ukontroversielt resultat. Den første antagelsen er at finansielle markeder er kjennetegnet ved fravær av systematisk arbitrasje. Fravær av systematisk arbitrasje betyr at det generelt ikke er mulig å få noe for ingenting. Det følger fra at finansielle markeder er konkurranseutsatte. Fravær av systematisk arbitrasje blir referert til som «Det grunnleggende teoremet til finansiell økonomi» (se for eksempel Dybvig og Ross, 1987). Med utgangspunkt i ikke-arbitrasje-betingelsen for finansielle markeder så kan vi utlede at det finnes en maksimal forventet Sharpe-rate som kan oppnås i markedet.
Den andre antagelsen er at finansielle markeder klarerer. Siden markeder klarerer og alle finansielle aktiva er eid av noen, vil markedsporteføljen oppnå denne høyeste forventete Sharpe-raten. Det beste forholdet mellom forventet avkastning og forventet risiko målt som standardavvik, som noen investor kan få ex ante, vil da være forventet avkastning på markedsporteføljen over forventet standardavvik på markedsporteføljen.12 Her spiller altså markedsindeksen en annen rolle i vår tilnærming enn som et sammenligningsgrunnlag slik vi diskuterte i underkapittel Sammenligningsportefølje. Vi må ikke nødvendigvis benytte markedsindeksen som et sammenligningsgrunnlag, men vi må benytte den for å få et estimat på markedsbaserte forventete avkastninger.
Til slutt er resultatet vi støtter oss på, at historiske andreordensmomenter gir mer presise estimat for forventete andreordensmomenter enn historiske førsteordensmomenter gir for forventete førsteordensmomenter. Med hensyn til andreordensmomenter så er det mulig å argumentere for at uendelig fin oppdeling av utvalgsrommet vil kunne fjerne all usikkerhet om estimater basert på historiske data. Førsteordensmomenter er imidlertid umulig å estimere presist (se for eksempel Maenhout, 2004; Pastor og Stambaugh, 2012; og Sargent og Stachurski, 2021).13 Med historiske data for avkastningsprosessen vil estimatene for standardavvik og korrelasjoner (andreordensmomenter) være langt bedre enn for forventete avkastninger (førsteordensmomenter).14
I denne artikkelen respekterer vi at historisk realisert avkastning ikke gir et godt estimat på fremtidig forventet avkastning. Vår fremgangsmåte er i stedet at gjennomsnittsinvestoren som investerer i de fire regionene, må holde den markedsvektede indeksen. Med denne indeksen oppnår gjennomsnittsinvestoren markedsindeksens forventete Sharpe-rate. Et estimat fra historiske data gir gode estimater på gjennomsnittsinvestorens forventninger til andreordensmomentene, det vil si standardavvikene til regionenes avkastning og kovariansene mellom dem. Dermed får vi et uttrykk vi kan løse for gjennomsnittsinvestorens forventninger til avkastningen i hver region.
I neste del går vi igjennom disse skrittene i detalj, men en leser som er mer interessert i de overordnede resultatene vi får enn detaljene i fremgangsmåten, kan hoppe over den delen.
Vi legger til grunn at beslutningen om å avvike fra markedsvektene via justeringsfaktorer for de forskjellige regionene ikke skyldtes at Finansdepartementet hadde andre forventninger til fremtidig avkastning enn det markedet priset inn. Deretter benytter vi de markedsbaserte forventete avkastningene til å sammenligne den forventete Sharpe-raten for markedsindeksen og for SPUs referanseindeks.
Den matematiske fremgangsmåten
For å karakterisere porteføljevalget til en investor som vil allokere mellom forskjellige regioner så lar vi og være vektorer hvor elementene er respektivt porteføljevektene på hver region og avkastningen utover risikofri avkastning for hver region. I tillegg lar vi være kovariansmatrisen for avkastningene i de fire regionene, slik at gir kovariansen mellom avkastningen i regionene og . Elementene på diagonalen (når ) gir da variansen i en regions avkastning.
For en portefølje sammensatt av investeringer i indekser fra forskjellige regioner får vi da følgende uttrykk for porteføljens forventete avkastning utover risikofri rente samt porteføljens standardavvik:
(10)
(11)
Porteføljevektene i enhver portefølje må summere til 1,
(12)
Gjennomsnittsinvestoren i markedet må nødvendigvis holde markedsporteføljen, og for gjennomsnittsinvestoren skriver vi dermed porteføljevektene wm. Disse markedsvektene er observerbare. Markedsporteføljen er som nevnt i forrige underkapittel, porteføljen som oppnår den høyeste oppnåelige forventete Sharpe-raten gitt våre antagelser om et marked fri for arbitrasjemuligheter som klarerer. Dermed vil små avvik fra markedsporteføljen ha neglisjerbar betydning for forventet Sharpe-rate. I vedlegg D viser vi at vi dermed får følgende uttrykk som karakteriserer likevekten i markedet:
(13)
Hvor er vektoren med markedsbaserte forventete avkastninger utover en risikofri rente for hver av regionene. Det siste vi trenger for å kunne løse dette ligningssystemet for disse forventete avkastningene er et estimat på kovariansmatrisen . Vi viser til diskusjonen ovenfor om estimering av første- og andreordensmomenter, og benytter historiske tall for å estimere denne matrisen. Dermed får vi tall for forventet varians for hver region og forventet kovarians for avkastningen mellom regionene, og vi kan løse for de markedsbaserte forventete avkastningene.15
Med en løsning for kan vi sammenligne porteføljer med forskjellige porteføljevekter. Vi ønsker å sammenligne markedsindeksen med SPUs referanseindeks. Derfor benytter vi porteføljevektene og sammen med og den estimerte kovariansmatrisen i uttrykkene i ligning (10) og ligning (11). Dermed kan vi beregne den forventete Sharpe-raten både for markedsindeksen og for SPUs referanseindeks.
Et siste poeng angående disse beregningene er at vi observerer porteføljevekter og vil beregne forventete avkastninger. Men på grunn av restriksjonen på porteføljevekter i ligning 12, så er det i praksis ikke ekstra informasjon i den siste porteføljevekten som følger automatisk av de andre vektene. Dermed har vi i praksis ligninger som skal løses for variabler. For å få dette til å gå opp gjør vi en antagelse om den forventete avkastningen for markedet som helhet og løser for hvordan denne forventete avkastningen fordeles på forventet avkastning i hver region. I våre beregninger sjekker vi at resultatene vi får i sammenligningene mellom forskjellige porteføljer ikke avhenger av denne antagelsen.
Evaluering av regionvektene valgt i 2012
I denne delen benytter vi fremgangsmåten presentert i del 1 og del 2 av rammeverket vårt til å gi et strukturelt estimat på verdiskapingen ved de valgte regionvektene sammenlignet med en portefølje med markedsverdivekter. Disse estimatene er kun basert på informasjon som var tilgjengelig i april 2012.
Forventet avkastning og risiko april 2012
Vi begynner med å løse ligningssystemet i ligning (13) for de forventete avkastningene som er konsistente med de observerte markedsvektene for de fire regionene. For å gjøre dette trenger vi tall for kovariansmatrisen Σ, og vi antar at en investor i april 2012 beregner denne matrisen basert på historiske tall for de siste 15 årene. Kovariansmatrisen kan beregnes fra korrelasjonsmatrisen og standardavvikene i avkastningene, så her presenterer vi disse tallene som har en mer intuitiv tolkning enn kovariansene.
Basert på månedlige tall fra januar 1997 til mars 2012 før vi følgende korrelasjonsmatrise:
(14)
Rekkefølgen på kolonnene og radene er utviklede markeder i Europa, utviklede markeder i Nord-Amerika, øvrige utviklede markeder i Asia og Oseania og fremvoksende markeder.
Vi får også følgende vektor for standardavvikene til avkastningene, σ:
(15)
Det siste vi trenger for å beregne markedets forventninger til avkastning i de fire regionene i april 2012, er en antagelse om forventet avkastning for markedet som helhet. En slik antagelse er nødvendig for å få et riktig antall ligninger, og påvirker selvfølgelig nivået på avkastningene vi beregner. Men det vi er interessert i er den relative sammenligningen for to forskjellige indekser, og for det formålet er denne antagelsen mindre viktig. I beregningene vi presenterer her setter vi .
De observerte markedsvektene fra 1. april 2012 finner vi i linje 2 i Tabell 1. Forventete avkastninger i de fire regionene som er konsistente med markedsvektene følger da av ligningssystemet i ligning (13). Resultatet for månedlige forventete avkastninger finner vi i Tabell 4.
Tabell 4: Markedsbaserte forventete avkastninger, månedlig, 1. april 2012.
| MSCI indeks | Europa | Nord-Amerika | Øvrige utviklede markeder | Fremvoksende markeder |
|---|---|---|---|---|
| E[R¯m] | 0,43 | 0,38 | 0,36 | 0,53 |
Tabellen viser at markedet priset inn høyere forventet avkastning i Europa enn i Nord-Amerika. Høyest forventet avkastning er imidlertid priset inn i indeksen for fremvoksende markeder. Ser vi på standardavvikene i ligning (15), ser vi at høyest forventet avkastning sammenfaller med høyest forventet variasjon.
Vi har nå tallene vi trenger for å beregne forventete avkastninger for forskjellige porteføljer via ligning (10) og forventete standardavvik via ligning (11). Dermed kan vi beregne forventete Sharpe-rater. Disse beregningene gjøres for markedsporteføljen med vekter fra linje to i Tabell 1 og for SPUs referanseindeks med vekter fra linje fire i samme tabell. Resultatene vises i Tabell 5.
Tabell 5: Forventete tall, annualisert, 1. april 2012.
| E[R¯p] (prosent) | Standardavvik (prosent) | Sharpe-rate (ex-ante) | |
|---|---|---|---|
| Markedsindeksen | 5,0 | 17,6 | 0,285 |
| Referanseindeksen | 5,1 | 18,0 | 0,284 |
Resultatene vi får viser at SPUs referanseindeks, som fra 2012 hadde en betydelig overvekt i europeiske aksjer i forhold til markedsindeksen, hadde en litt høyere forventet avkastning. Det forventete standardavviket var også høyere, og den forventete Sharpe-raten indikerer at avveiningen mellom avkastning og risiko dermed ble dårligere i SPUs referanseindeks. Forskjellen mellom de forventete Sharpe-ratene for de to porteføljene var imidlertid liten.16
Resultater fra evalueringskriteriene
For å evaluere betydningen av forskjellen i forventete Sharpe-rater på 0,001, benytter vi først uttrykket fra førsteordenstilnærmingen i ligning (4). Den gir et mål på hvor mye ekstra avkastning en investor som velger SPUs referanseindeks måtte få for å være indifferent mellom sin portefølje og markedsindeksen. Resultatet blir:
V1=(5,0-5,1)-(17,6-18,0)⋅0,285=0,014.
Avkastningen i SPUs referanseindeks må altså øke med 0,014 prosent per år for å gjøre investoren indifferent mellom denne indeksen og markedsindeksen når vi kun benytter en førsteordenstilnærming til investorens indifferenskurve.
Med fondsstørrelsen ved inngangen til 2012 og en aksjeandel på 60 prosent så er et anslag på det økonomiske tapet i kroner
3.312 milliarder⋅60 %⋅0,014 %=0,278 milliarder kroner
mens med fondsstørrelsen ved utgangen av 2020 og en aksjeandel på 70 prosent så er et anslag på det økonomiske tapet
10.914 milliarder ⋅70 % ⋅0,014 % = 1,07 milliarder kroner.
Snittet av disse er et tap på 674 millioner kroner hvert år eller 5,73 milliarder i løpet av åtte og et halvt år. Selv om dette er langt mindre enn 600 milliarder, er det fremdeles mye penger.
Vi kan også estimere verdiskapingen (eller verdidestruksjonen) av å avvike fra markedsvektene i SPUs referanseindeks med et mål basert på andreordenstilnærmingen til investorens indifferenskurve i ligning (9).
Med den første tilnærmingen til å kalibrere risikoaversjonen, får vi γ=1,84, når vi benytter tallene for markedsporteføljen fra Tabell 5.17 Som nevnt i diskusjonen om verdien for risikoaversjonsparameteret, får vi en relativt lav verdi med denne fremgangsmåten. Figur 3 viser indifferenskurven og kapitalmarkedslinjen med disse tallene og markerer punktene for markedsporteføljen og SPUs referanseindeks.
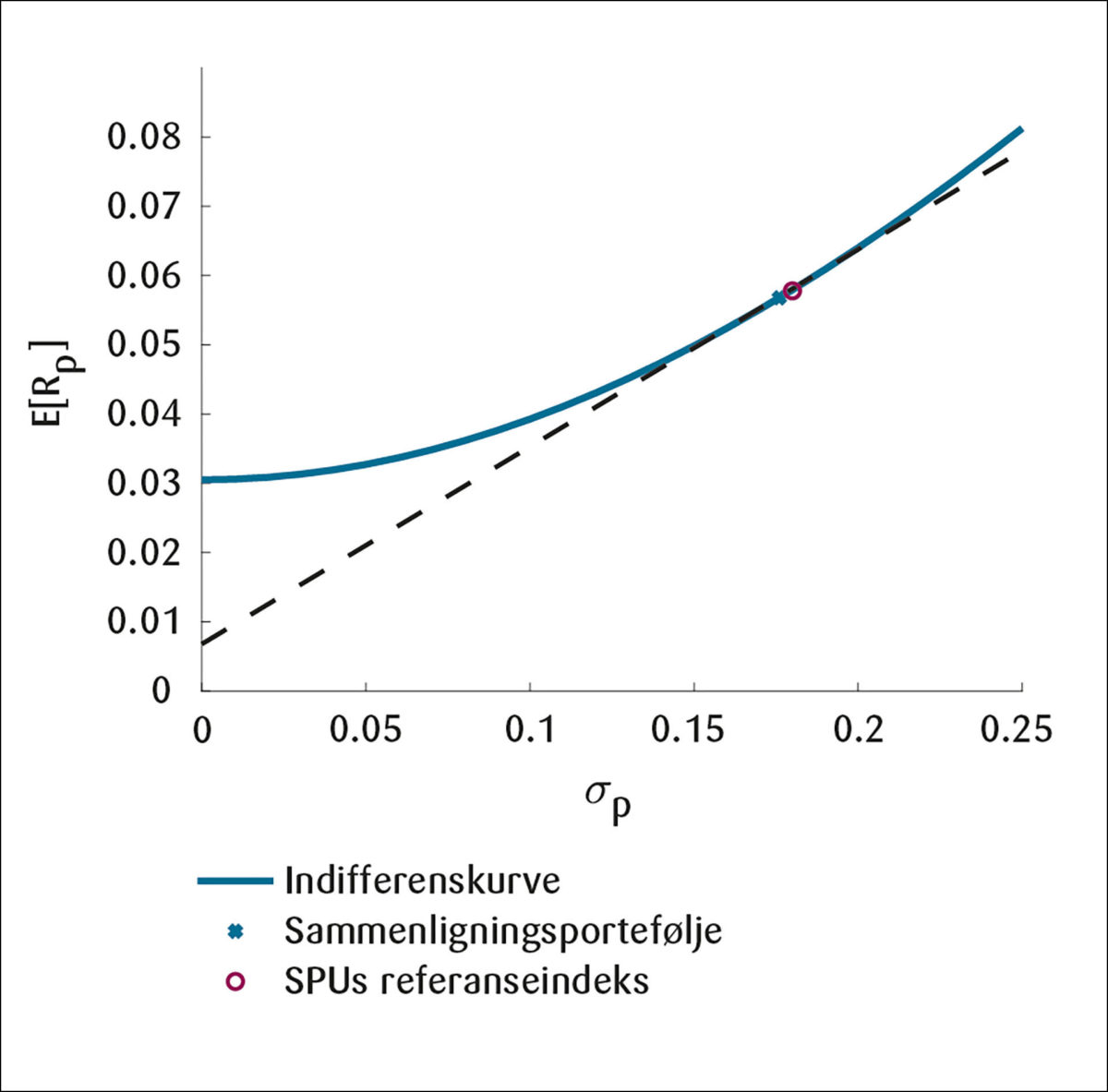
Figuren viser indifferenskurven for en investor som holder sammenligningsporteføljen. Vi har valgt å benytte markedsindeksen i sammenligningen, og den stiplede linjen har derfor et stigningstall lik SRm * Med en CRRA nyttefunksjon, er denne investorens risikoaversjon løst numerisk fra ligning (24), og når tallene fra Tabell 5 benyttes får vi γ=1,84.
Figur 3 viser at SPUs referanseindeks har høyere forventet avkastning og høyere standardavvik. Investorens indifferenskurve for SPUs referanseindeks ligger imidlertid såpass nært inntil kurven for markedsindeksen at den ikke vises i figuren. Når vi beregner sikkerhetsekvivalenter for begge disse kurvene får vi følgende estimat på verdidestruksjonen av allokeringsbeslutningen fra ligning (9):
V2=3,052-3,037=0,0154.
Med en andreordens tilnærming til nyttefunksjonen hvor risikoaversjonen er konsistent med en investor som holder markedsindeksen, får vi altså et litt høyere anslag på ex-ante kostnaden enn vi får med en førsteordens tilnærming. Snittet blir et tap på 743 millioner hvert år eller 6,32 milliarder kroner i løpet av åtte og et halvt år.
Vi påpekte imidlertid i underkapittelet Verdien for risikoaversjonsparameteret at en risikoaversjon kalibrert slik vi gjør ovenfor blir altfor lav til å være konsistent med risikopremien på aksjer. Ønsker vi å være konsistent med en høy risikopremie benytter vi i stedet en relativ risikoaversjon γ=22,5.18 Estimatet på verdidestruksjonen av allokeringsbeslutningen øker da til
V2H=0,077.
I denne modellen (som kan tilfredsstille ulikheten fra Hansen og Jagannathan (1991) beskrevet i Vedlegg C), vil altså avkastningen i SPUs referanseindeks måtte øke med 0,077 prosent per år for å gjøre investoren indifferent mellom denne indeksen og markedsindeksen. Gjennomsnittlig tap beregnet som ovenfor blir da 3,71 milliarder kroner per år eller 31,5 milliarder kroner i en periode på åtte og et halvt år.
Estimat for sannsynligheten til det realiserte utfallet
Den store forskjellen mellom de realiserte tallene for perioden fra 2012 til 2020 og de forventete tallene vi kom frem til når vi kun benyttet informasjon som var tilgjengelig på beslutningstidspunktet i 2012 gjør det naturlig å spørre hvor sannsynlig det realiserte utfallet var ex-ante? For å få et svar på dette kan vi simulere modellen vi har for avkastningsprosessen et høyt antall ganger. Fra de simulerte avkastningene for hver region, kan vi konstruere både markedsindeksen og referanseindeksen og se hvor ofte simuleringene fører til forskjeller i realiserte Sharpe-rater på 0,10 for de to indeksene (fra Tabell 3). Vi benytter da følgende modell:
(16)
Vektoren med realiserte avkastninger (utover risikofri rente) for hver region gis da i hver periode fra vektoren med forventete avkastninger utover risikofri rente og en vektor med sjokk til hver regions avkastning. Sjokkene hvor er den estimerte kovariansmatrisen. De månedlige avkastningene vi benytter, , vises i Tabell 5.
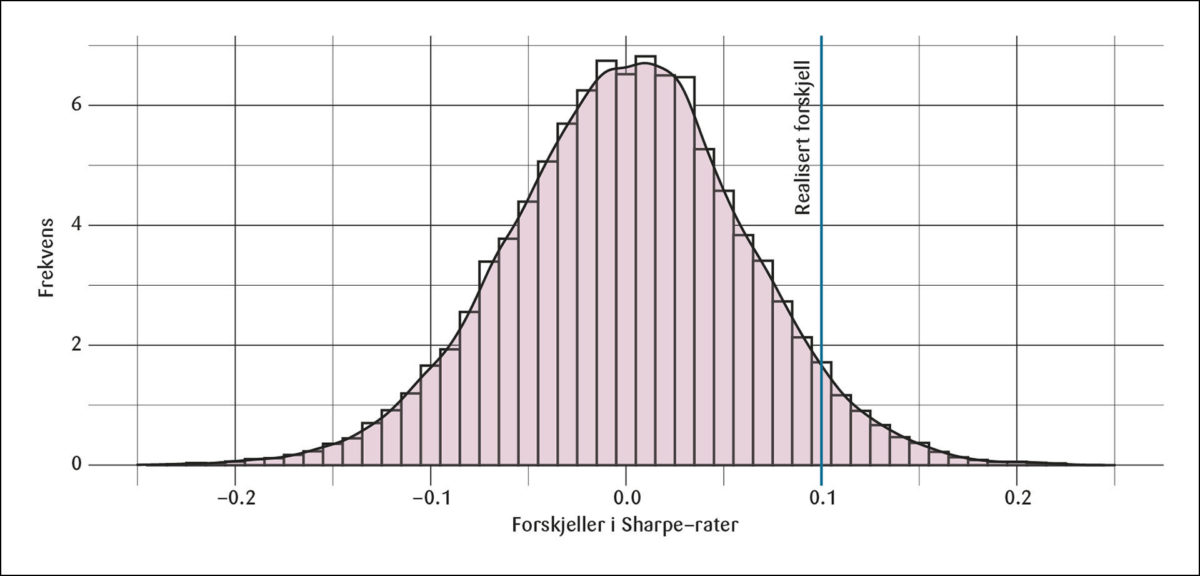
Figur 4 viser et histogram over forskjellene i de realiserte Sharpe-ratene for de to indeksene i 30.000 simuleringer av denne modellen. Forskjeller på 0,10 som vi observerer i data forekommer kun noen få ganger slik at dette tallet ligger helt ut i halen av fordelingen. Andelen av simuleringene som gir en forskjell høyere eller lik 0,10 er på kun 0,1 prosent. En modell for avkastningsprosessen hvor parameterne er konstante, gir dermed inntrykk av at det var veldig lite sannsynlig ex-ante at avviket fra markedsvektene i SPUs referanseindeks ville medføre et så stort tap som de realiserte tallene viser.
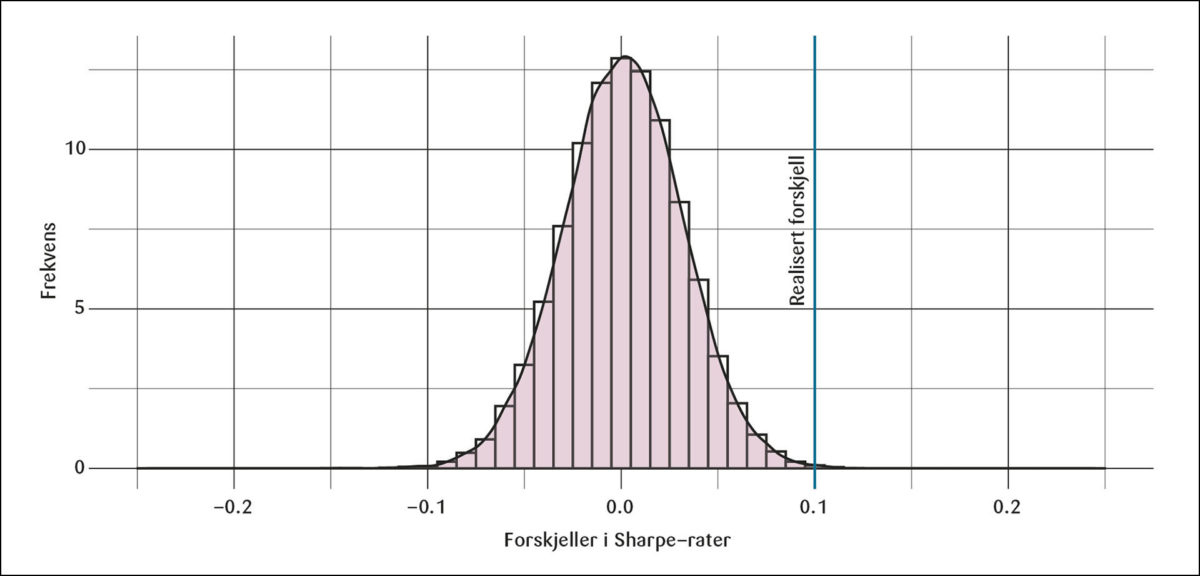
Histogram av forskjellen i realiserte Sharpe-rater i 30.000 simuleringer. I hver simulering genereres avkastninger for de fire regionene fra ligning (16). Så beregnes markedsindeksen, referanseindeksen og Sharpe-ratene for hver indeks fra de genererte avkastningene.
Vi har imidlertid allerede påpekt i del 2 av rammeverket at det er vanskelig å få et presist estimat for den forventete avkastningen i avkastningsprosessen. Det er derfor vi benytter fremgangsmåten beskrevet der for å beregne forventete avkastninger priset inn i markedet. Men selv med denne fremgangsmåten er det å legge til grunn at de forventete avkastningene er konstante over tid en veldig streng antagelse.
Utgangspunktet for Paster og Stambaugh (2012) er at parameterne i avkastningsprosessen er usikre, og at dette spesielt gjelder for den forventete avkastningen betinget på tilgjengelig informasjon. De estimerer derfor en avkastningsprosess hvor de tar hensyn til usikkerheten angående parameterne i prosessen og de tillater at den betingede forventete avkastningen kan variere over tid. Her benytter vi en forenklet versjon av modellen til Pastor og Stambaugh for å illustrere viktigheten av usikkerhet rundt den betingede forventete avkastningen. Dette gjelder selv når vi benytter vårt rammeverk for å beregne forventete avkastninger på et gitt tidspunkt.
Modellen vi benytter basert på Pastor og Stambaugh (2012) gis av følgende ligninger:
(17)
(18)
hvor notasjonen er at er realiserte avkastninger fra periode til for hver region, er de forventete avkastningene betinget på informasjonen som er tilgjengelig i periode , er en vektor med sjokk til hver regions realiserte avkastning, er de ubetingede forventete avkastningene, er sjokk til de betingede forventete avkastningene, og er en parameter som gir persistens i bevegelsene i de betingede forventete avkastningene.
Hvis vi setter og , får vi igjen modellen med konstante parametere i ligning (16). Det vi ønsker er å tillate usikkerhet i betingede forventete avkastninger ved å sette , men å gjøre dette på en måte som ikke øker den samlede usikkerheten i modellen. Derfor velger vi en parameter og skalerer ned usikkerheten i sjokket i de realiserte avkastningene ved å sette . Vi setter også og introduserer dermed usikkerhet rundt de betingede forventete avkastningene på en måte som gjør at den ubetingede kovariansmatrisen fortsatt er , den samme som i modellen med konstante parametere.
Vi tar igjen utgangspunkt i informasjon tilgjengelig i april 2012 og benytter den samme kovariansmatrisen som i evalueringen av regionvektene valgt i 2012, estimert på månedlige tall for de siste 15 årene. De ubetingede forventete avkastningene fra del 2 av rammeverket gis da i Tabell 4. Det som gjenstår for å illustrere viktigheten av usikkerhet rundt de betingede forventete avkastningene , er å velge parameterne og . I dette eksempelet har vi satt disse parameterne til og . Noe av usikkerheten i modellen skyldes da sjokk som endrer de betingede forventete avkastningene, og disse sjokkene er persistente.
Figur 5 viser et histogram over forskjellene i de realiserte Sharpe-ratene for markedsindeksen og referanseindeksen i 20.000 simuleringer av modellen med usikkerhet i forventete avkastninger. Figuren viser at forskjeller på 0,10 forekommer mye oftere når det er litt usikkerhet rundt parameterne i modellen. Andelen av simuleringene som gir en forskjell høyere eller lik 0,10 øker fra 0,1 prosent i modellen med konstante parametere til 5 prosent. Dette eksempelet illustrerer dermed at i en modell hvor det ikke antas at det finnes en konstant forventet avkastning, fremstår ikke de realiserte tallene like usannsynlige. Denne modellen indikerer imidlertid også at det var liten sannsynlighet ex-ante for å observere det store avviket mellom de realiserte Sharpe-ratene for den markedsvektede indeksen og SPUs referanseindeks som vi gjorde fra 2012 til 2020.
Histogram av forskjellen i realiserte Sharpe-rater i 20.000 simuleringer. I hver simulering genereres avkastninger for de fire regionene fra ligning (17) og ligning (18). Så beregnes markedsindeksen, referanseindeksen og Sharpe-ratene for hver indeks fra de genererte avkastningene.
Evaluering av regionvektene valgt i 2020
De nye justeringsfaktorene som ble foreslått i oktober 2020 innebærer at referanseindeksen fortsatt overvekter aksjer i Europa og undervekter aksjer i Nord-Amerika. Dette vises i nederste halvdel av Tabell 1. Som tabellen viser er imidlertid avviket mellom markedsvektene og de justerte vektene betydelig mindre enn de var tidligere. I denne delen benytter vi igjen de to delene av rammeverket og presenterer nok en sammenligning mellom markedsindeksen og SPUs referanseindeks. I denne sammenligningen benytter vi de nye vektene i SPUs indeks og markedsinformasjon tilgjengelig i oktober 2020.
Forventet avkastning og risiko oktober 2020
For å tallfeste elementene vi trenger for å løse ligning (13), gjentar vi antagelsen om at investoren beregner kovariansmatrisen basert på historiske tall for de siste 15 årene. Basert på månedlige tall fra oktober 2005 til september 2020 får vi følgende korrelasjonsmatrise:
(19)
Igjen er rekkefølgen på kolonnene og radene utviklede markeder i Europa, utviklede markeder i Nord-Amerika, øvrige utviklede markeder i Asia og Oseania og fremvoksende markeder.
Vi får også følgende vektor for standardavvikene i avkastningene, σ:
(20)
Som før kan vi beregne kovariansmatrisen i uttrykket for en porteføljes standardavvik i ligning (11) fra disse to størrelsene.
Vi gjentar også antagelsen om forventet avkastning utover den risikofrie renten for markedet som helhet og setter . De observerte markedsvektene fra 1. oktober 2020 finner vi i linje 4 i Tabell 1. Markedets forventete avkastninger i de fire regionene følger da av ligningssystemet i ligning (13). Resultatet for månedlige forventete avkastninger vises i Tabell 6. Tabellen viser at også i oktober 2020 priset markedet inn en høyere forventet avkastning i Europa enn i Nord-Amerika og høyest forventet avkastning i indeksen for fremvoksende markeder. Standardavvikene i ligning (20) viser at igjen sammenfaller høyest forventet avkastning med høyest forventet variasjon.
Tabell 6: Markedsbaserte forventete avkastninger, månedlig, 1. oktober 2020.
| MSCI indeks | Europa | Nord-Amerika | Øvrige utviklede markeder | Fremvoksende markeder |
|---|---|---|---|---|
| E[R¯m] | 0,45 | 0,40 | 0,34 | 0,48 |
Med disse tallene kan vi beregne forventete avkastninger for forskjellige porteføljer og forventete Sharpe-rater. Disse beregningene gjøres for markedsindeksen med vekter fra linje fire i Tabell 1 og for SPUs referanseindeks med vekter fra linje seks i samme tabell. Resultatene vi får er i Tabell 7.
Tabell 7: Forventete tall, annualisert, 1. oktober 2020.
| E[R¯p] (prosent) | Standardavvik (prosent) | Sharpe-rate (ex-ante) | |
|---|---|---|---|
| Markedsindeksen | 5,00 | 16,43 | 0,3043 |
| Referanseindeksen | 5,04 | 16,58 | 0,3041 |
Resultatene viser at forskjellene i forventete Sharpe-rater er betydelig mindre etter at de justerte vektene i referanseindeksen nærmet seg markedsvektene. Det er imidlertid fortsatt tilfellet at forventet avkastning og risiko er høyere i referanseindeksen, og at avveiningen mellom disse hensynene er bedre i markedsporteføljen.
Resultater fra evalueringskriteriene
Forskjellen i Sharpe-rater i våre beregninger er nå på kun 0,0002. Porteføljebeslutninger som tas i 2020 gjelder imidlertid for et mye større fond enn beslutningene som ble tatt i 2012. I tillegg har aksjeandelen i fondet økt slik at beslutninger som angår aksjeinvesteringene blir viktigere.
Vi tar igjen utgangspunkt i ligning (4) for å beregne verdiskapingen ved allokeringsbeslutningen om å overvekte aksjer i Europa basert på en førsteordenstilnærming til investorens indifferenskurve:
V1=(5,00-5,04)-(16,43-16,58)⋅0,3043=0,0056.
Fondets størrelse ved utgangen av 2020 og aksjeandelen på 70 prosent gir et anslag på det økonomiske tapet for avviket fra markedsvektene som følger:
10.914 milliarder⋅70 %⋅0,0056 %=0,428 milliarder.
Den estimerte kostnaden ved avviket fra markedsvektene som fortsatt ligger inne i referanseindeksen, basert på førsteordenstilnærmingen, ligger dermed på 428 millioner kroner per år.
Hvis vi i stedet gjentar beregningene basert på en andreordens tilnærming, må vi igjen først løse for et estimat på investorens risikoaversjon. Med tallene fra Tabell 7, får vi at γ=2,11. Når vi beregner sikkerhetsekvivalentene og benytter ligning (9), får vi et estimat på verdidestruksjonen av allokeringsbeslutningen i 2020:
V2=3,052-3,046=0,0059.
Vi får altså omtrent samme kostnadsanslag med andreordenstilnærmingen, og i kroner blir beløpet på 451 millioner kroner per år.
Vi gjentar også beregningene med en høy verdi for den relative risikoaversjonen og setter igjen γ=22,5. Da får vi et anslag på
I en modell som kan generere en høy risikopremie på risikable finansielle instrumenter vil altså kostnaden knyttet til avviket fra markedsvekter i SPUs referanseindeks fra 2020 og fremover være på 0,03 prosent eller 2,3 milliarder kroner per år.
Oppsumering
I denne artikkelen har vi presentert et generelt strukturelt rammeverk for å evaluere strategiske aktivaallokeringer og valg av referanseindekser. Deretter har vi anvendt dette rammeverket på beslutningen fra 2012 om hvordan SPUs aksjeportefølje skulle vektes mellom fire globale regioner. Vi evaluerte regionvektene i den strategiske referanseindeksen fra de ble vedtatt til de ble revidert i 2020.
NBIM (2020a) presenterer figurer som viser at sammenlignet med markedsverdivekter så medførte den valgte regionallokeringen i 2012 et realisert tap på omkring 600 milliarder kroner. Vårt estimat sammenfalt omtrent med dette, men faglig sett er ikke dette det relevante tallet. Ett utfall fra en stokastisk fordeling gir ikke et grunnlag for å fastslå om en beslutning var god eller dårlig eller for å gi et estimat på verdiskapingen forbundet med den ene beslutningen.
En strukturell tilnærming er nødvendig for å evaluere en strategisk allokeringsbeslutning. Under antakelsen om at markedsverdivekter var det teoretisk optimale valget av regionvekter i 2012, gir rammeverket vårt et laveste estimat på kostnaden ved den valgte regionallokeringen på i størrelsesorden 743 millioner kroner per år. Det vil si rundt 6,3 milliarder over perioden april 2012 til oktober 2020. Det høyeste estimatet vårt var omtrent fem ganger høyere: 3,71 milliarder kroner per år og totalt 31,5 milliarder kroner over åtte og et halvt år. Selv om dette er store beløp, er det viktig å merke seg hvor mye mindre de er enn den realiserte forskjellen i avkastning for den strategiske referanseindeksen sammenlignet med markedsporteføljen i denne perioden.
Nært relatert til at ett utfall fra en stokastisk fordeling ikke gir grunnlag for å fastslå om én beslutning var god eller dårlig, er å estimere hvor sannsynlig det ene realiserte utfallet var. Den realiserte forskjellen i Sharpe-rater mellom en portefølje med markedsvekter og en portefølje med referanseindeksens regionvekter, var i perioden 2012–2022 10 prosentpoeng. En utvidelse av rammeverket kan benyttes for å gi et anslag på sannsynligheten for en slik forskjell i realiserte Sharpe-rater. Når vi benytter en strukturell tilnærming som ikke hviler på en antagelse om at forventet avkastning er gitt og konstant, så er den estimerte sannsynligheten for utfallet omtrent 5 prosent.
I oktober 2020 ble det besluttet å redusere overvekten i aksjer som er notert i utviklede markeder i Vest-Europa og tilsvarende øke vekten i aksjer som er notert i utviklede markeder i Nord-Amerika. I fravær av analyser som viser noe annet, så er det rimelig å anta at markedsvekter var optimalt også i 2020. Det strukturelle rammeverket vårt gir et estimat på at kostnaden ved de nye vektene er i størrelsesorden mellom 450 millioner og 2,3 milliarder kroner per år.
Denne artikkelen peker også på de antakelig tre viktigste forholdene som avgjør størrelsen på estimatene for verdiskaping ved strategiske allokeringsvalg: (i) Den teoretisk optimale porteføljen: selv om markedsvekter er det analytiske utgangspunktet, kan dokumenterte egenskaper ved blant annet utestående fordringer og ikke-finansielle eiendeler potensielt lede til andre konklusjoner. (ii) Valg av nyttefunksjon: det er ikke åpenbart at den valgte parametriske klassen av nyttefunksjoner er riktig målestokk for å estimere verdiskapingen ved allokeringsvalg. Og (iii) avkastningsprosess: den parametriske strukturen på avkastningsprosessen påvirker de kvantitative estimatene for verdiskaping ved strategiske valg.
Avkastningen på finansielle porteføljer blir i stor grad bestemt av de langsiktige strategiske valgene som eier tar. SPU er et eksempel på dette: avkastning og risiko har nesten fullstendig blitt bestemt av referanseindeksen som er gitt av Finansdepartementet. Regionallokering er én av mange viktige beslutninger som inngår i referanseindeksen. Denne artikkelen gir et lite bidrag til å tenke prinsipielt og strukturelt på slike strategiske allokeringsbeslutninger.
Referanser
Back, K. E. (2017).Asset Pricing and Portfolio Choice Theory. 2. utgave. Oxford University Press.
Black, F. og R. Litterman (1992). Global portfolio optimization. Financial Analysts Journal 48 (5), 28–43.
Campbell, J. Y. (2018). Financial Decisions and Markets: A Course in Asset Pricing. Princeton University Press.
Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52 (1), 57–82.
Cochrane, J. H. (2005). Asset Pricing. Princeton University Press.
Cochrane, J. H. (2022). Portfolios for long-term investors. Review of Finance 26 (1), 1–42.
Dahlquist, M. og B. A. Ødegaard (2018). A review of Norges Bank’s active management of the Government Pension Fund Global. Rapport til Finansdepartementet.
Dybvig, P. og S. Ross (1987). Arbitrage. I J. Eatwell, M. Milgate og P. Newman (red.), The New Palgrave: a Dictionary of Economics, s. 100–106. Macmillan.
Fama, E. F. og K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33 (1), 3–56.
Fama, E. F. og K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116 (1), 1–22.
Meld. St. 17 (2011–2012). Forvaltningen av Statens pensjonsfond i 2011. https://www.regjeringen.no/no/dokumenter/meld-st-17-20112012/id676409/
Meld. St. 32 (2019–2020). Statens pensjonsfond 2020. https://www.regjeringen.no/no/dokumenter/meld.-st.-32-20192020/id2741487/
Hansen, L. P. og R. Jagannathan (1991). Implications of security market data for models of dynamic economies. Journal of Political Economy 99 (2), 225–62.
Hansen, L. P. og K. Singleton (1983). Stochastic consumption, risk aversion, and the temporal behavior of asset returns. Journal of Political Economy 91 (2), 249–65.
Henriksen, E. (2022). Planen var så god at finansiell risiko har tatt plassen til oljeprisrisiko. Samfunnsøkonomen 136 (4), 33–41.
Jensen, M. C. (1968). The performance of mutual funds in the period 1945–1964. Journal of Finance 23 (2), 389–416.
Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics 47 (1), 13–37.
Maenhout, P. J. (2004). Robust portfolio rules and asset pricing. Review of Financial Studies 17 (4), 951–983.
Markowitz, H. (2014). Mean-variance approximations to expected utility. European Journal of Operational Research 234 (2), 346–355.
Mehra, R. og E. C. Prescott (1985). The equity premium: A puzzle. Journal of Monetary Economics 15 (2), 145–161.
Merton, R. C. (1980). On estimating the expected return on the market: An exploratory investigation. Journal of Financial Economics 8 (4), 323–361.
Mossin, J. (1966). Equilibrium in a capital asset market. Econometrica 34 (4), 768–783.
NBIM (2020a). Investing with a mandate. Oslo: Norges Bank. https://www.nbim.no/en/publications/management-reviews/2020/the-funds-first-30-years/
NBIM (2020b). Investing in equities. Oslo: Norges Bank. https://www.nbim.no/en/publications/management-reviews/2020/the-first-20-years-of-investing-in-equities/
Pastor, L. og R. F. Stambaugh (2012). Are stocks really less volatile in the long run? Journal of Finance 67 (2), 431–478.
Sargent, T. J. (1987). Macroeconomic Theory. 2. utgave. Academic Press, Boston MA.
Sargent, T. J. og J. Stachurski (2021). Two modifications of mean-variance portfolio theory. Advanced Quantitative Economics with Python. https://python-advanced.quantecon.org/intro.html
Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19 (3), 425–442.
Stulz, R. (1981). A model of international asset pricing. Journal of Financial Economics 9 (4), 383–406.
Weil, P. (1989). The equity premium puzzle and the risk-free rate puzzle. Journal of Monetary Economics 24 (3), 401–421.
Vedlegg A: Alternativ antagelse om nyttefunksjonen
I andreordenstilnærmingen til indifferenskurven benytter vi en CRRA nyttefunksjon (konstant relativ risikoaversjon) fordi dette er et vanlig utgangspunkt i modeller i makroøkonomi og finans. Her antar vi i stedet at investoren har en nyttefunksjon med konstant absolutt risikoaversjon (CARA). Denne funksjonen har noen spesielle egenskaper som gjør at når den kombineres med normalfordelte avkastninger får vi et analytisk andreordensuttrykk for indifferenskurven. Dermed får vi med denne nyttefunksjonen et andreordensuttrykk som det er enda lettere å benytte i vår tilnærming.19
Her antar vi altså at investoren har en eksponentiell nyttefunksjon som gir konstant absolutt risikoaversjon. Det vil si at investorens nyttefunksjon over investorens formue («wealth»), W er:
(21)
hvor parameteren λ>0 gir graden av absolutt risikoaversjon. Vi kan da vise at hvis vi i tillegg antar at avkastningene følger en normalfordeling så er det å maksimere investorens forventete nytte det samme som å maksimere uttrykket:
(22)
Det vil si at vi kan fokusere på å maksimere den forventete avkastningen i investorens portefølje minus en kostnad forbundet med standardavviket i porteføljen. Kostnaden avgjøres av graden av risikoaversjon λ.20
Med denne antagelsen for nyttefunksjonen får vi altså et andreordens uttrykk for indifferenskurven uten at vi trenger en Taylor-tilnærming. Med denne funksjonelle formen for nyttefunksjonen gis sikkerhetsekvivalenten for en portefølje p av uttrykket i ligning (22). Investoren er indifferent mellom alle porteføljer som gir den samme forventete nytten med forskjellige kombinasjoner av forventet avkastning og standardavvik. Dermed får vi følgende for markedsindeksen og SPUs referanseindeks:
Den finansielle verdiskapingen målt ved dette andreordensuttrykket blir da
(23)
Dermed får vi et mål på kostnaden ved å avvike fra markedsvektene i SPUs referanseindeks som er en funksjon av investorens risikoaversjon. Som i første- og andreordenstilnærmingene i hovedteksten, velger vi også her å benytte markedsindeksen som et sammenligningsgrunnlag, men vi har ikke benyttet noen spesielle egenskaper ved markedsindeksen i utledningen av dette uttrykket for verdiskapningen. Dermed kunne vi også benyttet dette uttrykket for å sammenligne SPUs referanseindeks med en annen portefølje.
Uttrykket i ligning (23) er som uttrykket i ligning (9), en funksjon av investorens risikoaversjon . Men med dette valget av nyttefunksjonen er den førstederiverte av indifferenskurven gitt av uttrykket . Når vi benytter markedsindeksen som sammenligninsgrunnlag, så vil også denne indifferenskurven være tangent med kapitalmarkedslinjen ved denne porteføljen. Dermed kan vi enkelt kalibrere risikoaversjonen ved å sette den førstederiverte av indifferenskurven lik stigningstallet på kapitalmarkedslinjen som er gitt av , markedsporteføljens forventete Sharpe-rate. Uttrykket for blir da:
Vedlegg B: Den deriverte av en CRRA indifferenskurve
Det totale differensialet av ligning (8) gis av følgende uttrykk:
Utrykket følger av at vi har valgt å anta at markedsindeksen er det teoretisk optimale valget for denne investoren, så vi ser på indifferenskurven gjennom dette punktet. Som vi diskuterte i presentasjonen av førsteordenstilnærmingen til indifferenskurven, vil vi igjen ha at ved dette punktet må indifferenskurven være tangent til kapitalmarkedslinjen som har stigningstall gitt av markedets Sharpe-rate, . Dermed får vi følgende uttrykk:
(24)
Vi har da et uttrykk som vi kan løse numerisk for den ene ukjente for å få et estimat på investorens risikoaversjon. Figur 3 viser et numerisk eksempel.
Vedlegg C: Diskusjon om verdien for risikoaversjonen
Vi benytter som nevnt i underkapittelet Verdien for risikoaversjonsparameteret to forskjellige tilnærminger for å sette en verdi for γ. Den første tilnærmingen tar utgangspunkt i analyser av investorers porteføljevalg. Investorene har valget mellom forskjellige risikable finansielle instrumenter som har gitte verdier for risikofri rente og forventete risikopremier. I en slik tilnærming er det kun fokus på porteføljevalget og det gjøres ikke noe forsøk på å redegjøre for hvorfor de forventete avkastningene har de gitte verdiene.
Utgangspunktet er da en investor som kan investere i en lineær kombinasjon av risikofri rente og den markedsverdivektede porteføljen. For gitt risikoaversjonsparameter, risikofri rente, forventet risiko og avkastning for den markedsverdivektede porteføljen, så kan den optimale kombinasjonen (eller porteføljen) av risikofri rente og markedsporteføljen regnes ut.
Alternativt kan vi ta kombinasjonen (eller porteføljen) av risikofri rente og markedsporteføljen for gitt og beregne hva risikoaversjonsparameteret må være for at dette skulle vært et optimalt valg. I den ene av våre to beregninger av verdien for risikoaversjonen, beregner vi hva parameteret måtte ha vært for at investoren skulle velge å holde hele porteføljen i den markedsverdivektede verdensindeksen. Med nyttefunksjonen i ligning (6) og en indifferenskurve gitt av ligning (8), får vi et uttrykk for den deriverte av indifferenskurven evaluert ved punktet for markedsindeksen som vist i vedlegg B.21 Dermed kan vi løse numerisk for γ ved å sette dette uttrykket lik markedets Sharpe-rate som i ligning (24).
Den andre tilnærmingen er å ta utgangspunkt i litteraturen i finansiell økonomi som forsøker endogent å redegjøre for risikofri rente og de forventete avkastningene på risikable finansielle instrumenter og å knytte disse til makroøkonomiske størrelser som konsum og produksjon. Innenfor denne litteraturen er et viktig spørsmål hva som kan redegjøre for risikopremien som investorer har fått ved å investere i aksjer i forhold til den risikofrie renten. Historisk har denne risikopremien vært betydelig.
Siden Hansen og Singleton (1983), Mehra og Prescott (1985), og Weil (1989) har det vært kjent at det er vanskelig å gjøre rede for både risikopremien på aksjer, nivået på den risikofrie renten og investorers valg av aksjeandel i samme modell. Litt forenklet kan vi si at for å få en høy risikopremie vil modellen ha en høy verdi for risikoaversjonen. Investorer med høy risikoaversjon vil nemlig kreve en høy kompensasjon for å ta risiko. Men hvis investorer har veldig høy risikoaversjon vil deres portefølje ha en veldig lav aksjeandel siden de ikke ønsker å ta mye risiko. Det er dermed en utfordring å utvikle en modell som er konsistent både med en høy risikopremie og den graden av aksjeinvesteringer som vi observerer.
Ved å være noe mer tekniske, kan vi også vise til Hansen og Jagannathan (1991) som viste at følgende ulikhet kan utledes fra ikke-arbitrasje-betingelsen:
(25)
hvor er markedets prisingskjerne. En modell som skal forklare prisingen av risikable finansielle instrumenter bestemmer egenskapene til prisingskjernen. Via denne ulikheten stiller Sharpe-raten vi observerer i markedet et krav til disse egenskapene. Noe forenklet er kravet at prisingskjernen i modellen må være volatil nok (høy nok verdi for ) for at modellen skal kunne gi en høy risikopremie.
CRRA nyttefunksjonen i ligning (5) som ofte benyttes i makroøkonomi og finansiell økonomi, gir følgende uttrykk for prisingskjernen når nytten gis av konsum i stedet for formue:
(26)
Her er konsum og diskonteringsfaktoren. I ligning (25) så er både Sharpe-raten på høyre side og dynamikken til konsum direkte observerbar. Men i forhold til den variasjonen som er nødvendig for at prisingskjernen kan tilfredsstille ligning (25), så er konsumveksten vi observerer i utviklede markeder altfor lav. Den eneste måten å tilfredsstille ulikheten er dermed hvis verdien for er veldig høy.
Den eksakte verdien for γ som man ender opp med vil variere med hvilket marked og hvilken tidsperiode man ser på, men denne tilnærmingen vil typisk gi en relativt høy verdi for risikoaversjonsparameteret. Verdien blir gjerne på størrelsesorden rundt 22,5 eller enda høyere. En så høy grad av risikoaversjon kan generere realistiske risikopremier på risikable finansielle instrumenter, men vil samtidig gi en altfor høy risikofri rente og en veldig liten aksjeandel i porteføljen.
Vi rapporterer derfor også estimater på verdiskapingen for allokeringsbeslutninger fra en modell med en CRRA nyttefunksjon og γ=22,5, vel vitende om problemene ved en slik modell.
Vedlegg D: Likevekt i markedet
Gjennomsnittsinvestoren, som i dette tilfellet kun investerer i indekser fra et sett med regioner, holder den markedsvektede indeksen for disse regionene. Vi observerer markedsvektene .
Siden den markedsvektede indeksen oppnår den høyeste forventete Sharpe-raten, så må små avvik fra markedsvektene nødvendigvis ha liten effekt på den forventete Sharpe-raten. Uttrykket for den forventete Sharpe-raten kan ansees som en funksjon av , og den deriverte av denne funksjonen må dermed være lik null. I vår vektornotasjon gir det oss følgende betingelse:
Når vi løser for den deriverte i dette uttrykket, får vi følgende ligningssystem:
Uttrykket utenfor sløyfeparentesen kan skrives som følger:
Dermed kan vi ignorere dette leddet og løse følgende sett med ligninger:
Dette er det samme ligningssystemet som i ligning (13).
Fotnoter:
- Takk til deltagerne på seminar i regi av Oslo makrogruppe (OMG), hos Statistisk sentralbyrå, hos Finansdepartementet, ved Handelshøyskolen BI og til blant andre Thomas von Brasch, Ingrid Huitfeldt, Hans Hvide, Thore Johnsen, Patrick Konermann, Jens Kværner, Knut Anton Mork, Martin Schmalz, en anonym fagkonsulent og redaktør Rune Jansen Hagen for gode kommentarer. Espen Henriksen mottok støtte av Finansmarkedsfondet under prosjekt 294398. ↩︎
- Se figur 18 på side 45 og omtalen på side 43 i NBIM (2020a). ↩︎
- Se NBIM (2020b). ↩︎
- Meld. St. 32 (2019–2020), boks 3.1, side 48. ↩︎
- I Norges Banks brev til Finansdepartementet 2. februar 2012, signert Øystein Olsen og Yngve Slyngstad, skriver de: «Fondets regionvekter, med en høy andel investert i Europa, har vært motivert ut i fra et mål om å reflektere Norges fremtidige importmønster», https://www.nbim.no/no/publikasjoner/brev-til-finansdepartementet/2012/statens-pensjonsfond-utland–strategisk-referanseindeks-for-aksjer/. ↩︎
- https://www.nbim.no/no/publikasjoner/brev-til-finansdepartementet/1997-2000/forslag-til-retningslinjer-for-statens-petroleumsfond/ ↩︎
- SPUs referanseindeks for aksjer tar utgangspunkt i indekser fra FTSE Russell. Fordi det er svært stort overlapp mellom indekser levert av FTSE og MSCI og fordi data for indekser fra MSCI er lettere tilgjengelige, benytter vi indekstall fra MSCI for denne analysen. Samme tilnærming benytter Meld. St. 32 (2019–2020) (se boks 3.2). ↩︎
- Månedlige tall konverteres til årlige ved å multiplisere avkastningen med 12 og standardavviket med √12. ↩︎
- Tallene er tilgjengelige på https://www.nbim.no/no/markedsverdi/. ↩︎
- I motsetning til Stulz (1981) er det ikke nødvendig å ta hensyn til segmentering siden indeksene som SPU benytter allerede er definert over det investerbare investeringsuniverset. ↩︎
- I et innlegg om regionfordelingen til SPU i Dagens Næringsliv 22. juni 2021 omtalte Trym Riksen markedsverdivekter som «byggnormen for porteføljekonstruksjon». ↩︎
- Kapitalverdimodellen (Sharpe, 1964, Lintner, 1965, Mossin, 1966) er et eksempel på en modell hvor markeder klarerer og markedsporteføljen oppnår den høyeste forventete Sharpe-raten. Forventet porteføljeavkastning er da E[Rp] = Rf + E[SRm] ∙ σp, hvor Rf er risikofri rente, E[SRm] er den forventete Sharpe-raten til markedsporteføljen og σp er forventet risiko på porteføljen. ↩︎
- Et annet eksempel er Merton (1980) som viser til at «…the estimates of variances and covariances from the available time series will be much more accurate than the corresponding expected return estimates» (side 326). ↩︎
- Det er også økonomiske-teoretiske argumenter for at historisk realisert avkastning ikke gir et godt anslag på fremtidig forventet avkastning. Se for eksempel Henriksen (2022, side 38–39) som viser videre til blant andre Cochrane (2022). ↩︎
- Prosedyren vår for å estimere hva forventet avkastning var, har fellestrekk med tilnærmingen til Black og Litterman (1992) ved at begge utnytter informasjonen i markedsklarering i konkurranseutsatte finansielle markeder. ↩︎
- Merk at hvis vi i stedet antar en forventet markedsavkastning på 4 prosent får vi forventete Sharpe-rater på 0,228 og 0,227 for de to porteføljene. En forventet markedsavkastning på 6 prosent gir forventete Sharpe-rater på 0,342 og 0,341. Denne antagelsen påvirker dermed ikke resultatet om en litt høyere forventet Sharpe-rate i markedsindeksen. ↩︎
- Detaljene om hvordan vi med denne fremgangsmåten løser ligning (26) for en verdi for γ er beskrevet i vedlegg B og vedlegg C. ↩︎
- Se vedlegg C for en detaljert diskusjon av kalibreringen av γ. ↩︎
- Vi henviser likevel dette til et vedlegg fordi CARA nyttefunksjonen også har egenskaper som er lite realistiske. ↩︎
- For en detaljert utledning av ligningene vi benytter her, se for eksempel Sargent (1987). ↩︎
- Merk at dette også gjelder hvis vi i stedet velger en CARA nyttefunksjon og kalibrerer verdien for absolutt risikoaversjon, λ. Som vist i vedlegg A gis denne kalibreringen av λ = SR m/σ m. ↩︎

