Bør man maksimere forventet nytte?
I vurderingen av lite sannsynlige, men katastrofale hendelser blir det av enkelte anbefalt å fravike forventet nytte som beslutningskriterium. Innenfor en enkel beslutningssituasjon vurderer vi forventet nytte opp mot andre beslutningsregler som har vært foreslått. Forventet nytte fungerer godt overfor katastrofer på sektornivå. I beslutninger som gjelder nasjonaløkonomiske katastrofer kan økonomisk teori hjelpe oss et stykke på vei, men til slutt må man bruke skjønn innenfor et innsnevret mulighetsområde.
Bør man maksimere forventet nytte?1
Beslutningsregler overfor katastrofale hendelser
1. INNLEDNING
I boken Et veddemål tar Per Lønning (1980) for seg «Pascals veddemål», utgitt i 1670. Pascals veddemål handler om en hendelse som Pascal mener kan ha svært lav, men endelig sannsynlighet (selv om han tror mest på 50:50), nemlig Guds eksistens, og som har uendelig høy konsekvens hvis man velger å tro. Pascal bruker forventet nytte til å argumentere for at man må tro: Men her er det en evighet av liv i lykke… å vinne, en sjanse for vinning mot et begrenset antall sjanser for tap, og det som du setter inn, er begrenset. Dette gjør spillkalkylen helt opplagt overalt hvor det dreier seg om det uendelige og hvor det ikke står et uendelig antall tapsmuligheter mot muligheten for å vinne. Her er ingenting å oppveie, her må man satse det hele.
Også i våre dager er teori for beslutninger under usikkerhet knyttet til forventet nytte. Den presenteres som en normativ teori (individer og samfunn bør maksimere forventet nytte) og med noe mindre selvtillit presenteres den som en deskriptiv teori (individer og samfunn maksimerer faktisk forventet nytte). Det er den normative betydningen som interesserer oss her, og vi anlegger et samfunnsperspektiv.
Spørsmålet blir da: Bør samfunnet maksimere forventet nytte? De senere årene er det oppstått en diskusjon knyttet til hendelser med lav sannsynlighet for å inntreffe, men høy konsekvens dersom de faktisk inntreffer. På engelsk kalles de HILP-hendelser (high impact, low probability). NOU 2012:16 diskuterte dem under navnet katastrofer og konkluderte at «hvis sannsynligheten er ikke-neglisjerbar, eller en ikke kan fastslå at den er det, vil standard analysemetode kunne undervurdere, kanskje i betydelig grad, kostnaden knyttet til at samfunnet utsettes for en ukjent grad av katastroferisiko» (NOU 2012:16, kap 8.6).
Dersom samfunnet ikke bør maksimere forventet nytte, i hvert fall ikke stilt overfor HILP-hendelser, vil det ha praktiske konsekvenser. For eksempel vil en ikke kunne stole på tidligere anbefalinger fra den anvendte økonomens arbeidshest, samfunnsøkonomisk analyse. Utredningsinstruksen for staten krever at alle større statlige virkemidler og tiltak skal gjennomgå samfunnsøkonomisk analyse. Staten investerer alene for 150 milliarder kroner i året. Potensielt kan et annet beslutningskriterium enn forventet nytte føre til at betydelige deler av samfunnets ressurser disponeres på en annen måte.
For å vurdere om samfunnet bør maksimere forventet nytte stilt overfor HILP-hendelser, må man kjenne alternativene. Hensikten med denne artikkelen er å studere konsekvensene av noen alternative beslutningsregler. Vi innleder med å diskutere hva som utgjør en HILP-hendelse. Deretter stiller vi opp en enkel modell med tre tilstander og drøfter beslutningsregler foreslått i litteraturen. Virker de rimelige? Er samfunnet tjent med å legge dem til grunn i stedet for forventet nytte? Det er hovedtemaet i artikkelen, som bygger på tidligere arbeid i Vista Analyse, særlig Hoel og Vennemo (2018) og Hoel (2021).2
2. EN HILP-HENDELSE ER EN KATASTROFE PÅ NASJONALT NIVÅ
De siste årene har vist at HILP-hendelser forekommer eller med nød og neppe unngås. Koronapandemien sendte oss hjem og kunne gitt mange flere dødsfall om den var mer smittsom. Russlands invasjon av Ukraina kan utløse en global HILP-hendelse. Aggresjonen mellom USA og Kina kan utløse en eller flere HILP-hendelser. Finanskrisen i 2008 ga alvorlige konsekvenser og kunne blitt langt verre. Posner (2004), Taleb (2007) og Weitzman (2011) argumenterer for at sannsynligheten for katastrofale hendelser for verden og nasjonene er større enn de fleste er klar over.
Mange HILP-hendelser er mulig å kjenne igjen når man ser dem, men hva er det som kjennetegner dem? Noen mener at hendelser på sektornivå kan være HILP-hendelser. Sintef (2016) skriver:
«Samfunnet er i økende grad avhengig av sikker og stabil straumforsyning. Hvor essensiell en rolle elektrisitet har er kanskje mest åpenbart når det en sjelden gang inntreffer omfattende og langvarige strømbrudd (“blackouts”). Sannsynligheten for at slike strømbrudd inntreffer kan være veldig liten, men dersom de inntreffer er de samfunnsmessige konsekvensene veldig store. Slike ekstraordinære hendelser blir derfor også kalt HILP-hendelser (“High-Impact Low-Probability events”).»
Et strømbrudd som er stort i omfang og/eller tid er opplagt en alvorlig (high impact) hendelse. En kan likevel spørre om et slikt strømbrudd er så alvorlig at det kan kalles en «katastrofe»; og spesielt om alvorlighetsgraden tilsier at standard økonomiske analyser ikke uten videre kan brukes for å analysere slike hendelser.
For å vurdere et alvorlig strømbrudd i et bredere perspektiv skal vi se på et hypotetisk eksempel. De nøyaktige tallene i eksempelet er ikke viktige, men deres størrelsesorden illustrerer poengene. Anta at et strømbrudd innebærer at 1 million husholdninger mister strøm i ett døgn om vinteren.
Anta videre at hver husholdning i snitt bruker 50 kWh i løpet av et slikt døgn (Dalen og Halvorsen, 2022). I så fall innebærer et slikt strømbrudd et bortfall av totalt 50 GWh.
Eksempelet illustrerer en svært stor og alvorlig hendelse. Men bør en omtale en slik hendelse som en katastrofe3? For å svare på dette gir vi et grovt anslag på hva hendelsen innebærer i kroner. Det virker rimelig at de aller fleste husholdninger vil være fornøyd alt i alt dersom de opplever en slik hendelse og samtidig får en kompensasjon på 10.000 kroner.4 I så fall innebærer dette at kostnaden av hendelsen er (maksimalt) 10 milliarder kroner (svarende til 200 kroner per uteblitt kWh). Dette er et stort tap, men er det en katastrofe? Vi kan sammenligne med tre andre hendelser som også gir store tap.
- Ett år med 0,5 pst. negativt avvik fra trend-BNP. Det gir et tap på mer enn 25 milliarder kroner (Norges BNP i 2024 er i Nasjonalbudsjettet anslått til ca. 5300 milliarder kroner).
- Et fall i verdien på oljefondet på 0,2 pst. Det gir et tap på ca. 32 milliarder kroner.5
- En nedjustering av fremtidig oljeprisbane med 1 dollar per fat (dvs. ca 1,2 pst.). Tapt nåverdi for staten er nesten 40 milliarder kroner (nåverdien av fremtidige inntekter fra salg av olje og gass anslås i Nasjonalbudsjettet 2022 til ca 3200 milliarder kroner).
Alle disse hendelsene innebærer store tap for Norge, men kan neppe kalles katastrofer. For at en hendelse i kraftsektoren skal konkurrere med disse, må man tenke seg at 1 million mennesker mister strømmen i tre døgn (gir 30 milliarder i tap hvis kostnaden øker proporsjonalt med varigheten av strømbruddet), om lag det samme som i sammenligningseksempel 1 og 2. Men for å fortjene betegnelsen nasjonaløkonomisk katastrofe må hendelsen etter vår vurdering være en god del større enn dette også.
I NOU 2012: 16 står det (kap 8.3):
«Definisjonen av katastrofe avhenger åpenbart av hvilket nivå vi betrakter (…) En krig eller en okkupasjon er åpenbart en katastrofe på nasjonalt nivå, likeså et terrorangrep som det Norge opplevde 22. juli 2011, eller en pandemi med store mengder døde. På globalt nivå vil selv et terrorangrep på norsk jord falle utenom katastrofebegrepet.»
Hvilket nivå skal vi så betrakte? I samfunnsøkonomiske analyser betrakter vi det nasjonale nivået. Det betyr at katastrofer på sektornivå, som et omfattende strømbrudd, ikke rettferdiggjør andre beslutningsregler enn maksimering av forventet nytte. Det avgjørende er om slike «sektorkatastrofer» når opp til å bli katastrofer på nasjonalt nivå. På den annen side blir det et vurderingsspørsmål hva som utgjør en katastrofe på nasjonalt nivå.
Globale katastrofer vil i regelen også være katastrofer på nasjonalt nivå. Pandemien er et nylig eksempel. Men her kommer det inn et annet forhold, nemlig at det ikke er alle globale katastrofer Norge kan gjøre noe med. Vi kan ikke forhindre dem, og vi kan i noen tilfeller heller ikke redusere konsekvensene av dem. Inntil nylig kunne verdenssamfunnet ikke forhindre kollisjon mellom jorda og en stor meteor/asteroide, og Norge kan det fortsatt ikke. En hendelse som klimasjokket i år 535-536, der det antas at så mye som halvparten av Norges befolkning døde ut, vil verdenssamfunnet fortsatt ikke kunne gjøre så mye med.6
Hvis både sannsynligheten for en katastrofe og konsekvensen av denne er eksogent gitt, er det ikke så mye mer å si om saken. Verken forventet nytte eller noe annet kommer til anvendelse, fordi det er ingen valg. Det interessante tilfellet er når en beslutningstager med en viss sannsynlighet enten kan påvirke sannsynligheten for katastrofen eller konsekvensen av katastrofen.
I resten av artikkelen antar vi at det finnes en tilstand der beslutningstageren kan påvirke konsekvensen av en katastrofe, og en tilstand der beslutningstageren ikke kan det. For å belyse poengene så enkelt som mulig bruker vi hele veien et enkelt beslutningsproblem under usikkerhet.
3. ET ENKELT BESLUTNINGSPROBLEM UNDER USIKKERHET
Som regel vil det være ulike typer hendelser som kan føre til en katastrofe, og ulike typer tiltak som kan redusere sannsynlighetene for hendelsene, og kanskje også konsekvensene av katastrofen. I vår videre analyse ser vi på en svært forenklet situasjon hvor det bare er én type hendelse og ett tiltak. Vi bruker følgende notasjon for ingrediensene i analysen:
• y = inntekt uten tiltak og uten katastrofe
• T = tapet dersom katastrofen inntreffer
• p+q = sannsynlighet for katastrofen uten tiltak
• q = sannsynlighet for katastrofen til tross for tiltak
• p = sannsynlighetsreduksjon som følge av tiltak
• k = kostnad av tiltak (k<T)
• K = maksimal kostnad k for at tiltaket bør gjennomfø-
res (følger av analysen)
Dersom tapet knyttet til katastrofen bare innebærer tap av materielle verdier, er tapet T i prinsippet en veldefinert størrelse. Mange katastrofer gir også tap av liv og helse, og da er det ikke opplagt hvordan en skal beregne T. «Standardmetoden» for tap av liv er å bruke verdien av et statistisk liv (VSL), se f.eks. DFØ (2023). Det er ikke opplagt at VSL gir et «riktig» bilde av konsekvensene av en katastrofe, særlig ikke «for tiltak der virkninger for liv og helse er en hovedkonsekvens, spesielt der tiltakene innebærer betydelige risikoendringer for enkeltpersoner og/eller det er kjent hvem som særlig berøres…» (NOU 2012: 16). Omregning av virkninger på liv og helse til økonomiske størrelser er et viktig og komplisert spørsmål, men ligger på siden av hva vi drøfter i denne artikkelen. Vi tar derfor i den videre analysen størrelsen på tapet T som veldefinert og kjent og regnet i kroner.
«Ex post»-konsekvensene av ulike beslutninger er illustrert i Tabell 1 nedenfor.

De to linjene gir de to valgmulighetene beslutningstager har (tiltak og ikke-tiltak). For hvert valg gir kolonnene de tre mulige tilstandene som kan inntreffe (gitt ved overskriftene). Første kolonne angir nettoinntekt dersom det ikke blir noen katastrofe (uavhengig av valget tiltak eller ikke-tiltak). For denne tilstanden gir tiltak lavere nettoinntekt (y-k) enn ikke-tiltak (y), siden en har investert unødig (k > 0). Det samme er tilfellet for tilstanden gitt ved den tredje kolonnen, siden katastrofen da vil skje uansett. Inntreffer derimot tilstanden gitt ved den andre kolonnen, er inntekten høyest dersom en har valgt tiltak (forutsatt k < T), siden en da har unngått kostnaden T som en ville fått ved ikke-tiltak.
Beslutningsproblemet illustrert med Tabell 1 er et typisk eksempel på beslutning under usikkerhet. Dersom en med sikkerhet visste at tilstand (kolonne) 1 eller 3 ville inntreffe, ville det beste valget være ikke-tiltak. Og tilsvarende hvis en med sikkerhet visste at tilstand (kolonne) 2 ville inntreffe; da ville det beste valget være tiltak. Imidlertid vet ikke beslutningstageren på beslutningstidspunktet hvilken tilstand som vil inntreffe, og må derfor treffe en beslutning under usikkerhet om fremtidig tilstand.
I beslutningsproblemet som blir drøftet, er det bare tre mulige tilstander med tilhørende sannsynligheter. I virkeligheten vil det også knytte seg usikkerhet til omfang og kostnader knyttet til katastrofen, og trolig også til kostnaden av tiltak. Formelt kan dette analyseres ved å øke antall mulige tilstander. En kan også utvide antall tiltak, hvor noen av tiltakene reduserer kostnaden K dersom en katastrofe inntreffer. Slike utvidelser av analysen ville føre til mer notasjon og bli mindre oversiktlig, men ville ikke gi noe prinsipielt nytt. Vi begrenser oss derfor til det enkle beslutningsproblemet illustrert ved Tabell 1.
4. FORVENTET GEVINST OG FORVENTET NYTTE SOM SAMMENLIKNINGSGRUNNLAG
Selv om vi er interessert i andre beslutningsregler, er det praktisk å ha forventet nytte som sammenlikningsgrunnlag i analysen. Innledningsvis kan vi minne om at teorien om forventet nytte ikke forutsetter frekvensbaserte («objektive») sannsynligheter. Det er tilstrekkelig at beslutningstageren har et konsistent sett med subjektive sannsynligheter (Savage, 1954). Et viktig poeng er at kunnskapsgrunnlaget som sannsynlighetene bygger på, er viktig for hvilken tiltro en skal ha til slike sannsynligheter. Et svakt kunnskapsgrunnlag kan øke den subjektive sannsynligheten for usannsynlige hendelser sammenliknet med en «ex ante»vurdering.7 Kunnskapen sannsynlighetene bygger på er derfor en viktig del av beslutningsprosessen. Vi går ikke mer inn på kunnskapsgrunnlaget for sannsynligheter i resten av dette avsnittet, og skiller her heller ikke mellom subjektive og objektive sannsynligheter.
I alminnelig nytte-kostnadsanalyse antas ofte risikonøytralitet. I så fall sier analysen at tiltak bør velges fremfor ikke-tiltak dersom forventet verdi av tiltak er større enn forventet verdi av ikke-tiltak. Fra Tabell 1 er det rett frem å se at dette innebærer at tiltak bør velges hvis og bare hvis k < pT. Tolkningen er rett frem. Uten tiltak er forventet tap lik (p+q)T, men med tiltak er forventet tap lik qT. Differansen pT er gevinsten av tiltaket, som må overstige tiltakskostnaden k for at tiltaket skal være lønnsomt. I dette tilfelle har vi altså at K = pT (hvor K som sagt er største akseptable verdi av k).
Konklusjonen modifiseres hvis vi maksimerer forventet nytte og legger til grunn risikoaversjon. Risikoaversjon betyr at vi har en konkav nyttefunksjon u(x)8, slik at forventet nytte av tiltak og ikke-tiltak er gitt ved
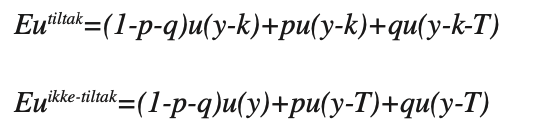
Vi finner K som den verdien av k som gjør disse to forventede nyttene like. Risikoaversjon (dvs. u’’<0) innebærer at pT < K < T, der vi minner om at K er største akseptable verdi av k.9 Den nøyaktige verdien av K avhenger selvsagt av spesifiseringen av funksjonen u(x). Vi skal anta at vi har en funksjon med konstant relativ risikoaversjon, som innebærer at funksjonen har formen u(x) = (1 – r)⁻¹ x¹⁻ʳ hvor parameteren r måler graden av risikoaversjon.10
Med risikoaversjon vil altså analysen anbefale tiltak som er dyrere enn forventet inntektsgevinst (K > pT). Forholdet (K – pT) / pT kan tolkes som en relativ forsikring. Et interessant spørsmål for den videre analysen er hvor stor denne forsikringen vil være. Det viser seg, kanskje ikke overraskende, at svaret på dette spørsmålet avhenger av hvor kraftig risikoaversjon samfunnet har. Et annet viktig resultat er at forsikringspremien (K – pT) / pT er større jo større T / y er, dvs. jo større det potensielle tapet er relativt til inntekten. For små verdier av T / y (dvs. tap som definitivt ikke kan kalles katastrofer) er forsikringspremien tilnærmet lik null, dvs. risikoaversjon har nesten ingen betydning.
I litteraturen kan man finne støtte for både små og store verdier for relativ risikoaversjon. En metastudie av Eliminejad mfl. (2022) konkluderer at «after correction for the bias, the literature suggests a mean risk aversion of 1 in economics and 2-7 in finance contexts». Gandelman og Hernandez-Gurillo (2015) skriver at «Probably the most commonly accepted measures of the coefficient of relative risk aversion lie between 1 and 3, but there is a wide range of estimates in the literature—from as low as 0.2 to 10 and higher.» Estimatene her er for individer, men er relevante for samfunnets preferanser når disse på en eller annen måte er basert på individ-preferanser.
Vi har regnet på et eksempel der vi lar katastrofen utgjøre et halvt års BNP, men sannsynligheten er liten, bare en tusendel (dvs. q + p = 0,001). Vi antar altså at T = y / 2, og vi har satt y = 5300 mrd. kroner, som er Nasjonalbudsjettets anslag for BNP i 2024. Dette er representativt for en meget usannsynlig, verdensomspennende katastrofe av typen omfattende atomkrig, som vi får håpe inntreffer hvert tusende år eller sjeldnere. Vi antar videre at et tiltak fra Norges side reduserer sannsynligheten med en titusendel (dvs. p = 0,0001). Vi har regnet ut K og forsikringspremien (K – pT) / pT både for risikonøytralitet og to tilfeller av risikoaversjon, se tabell 2.
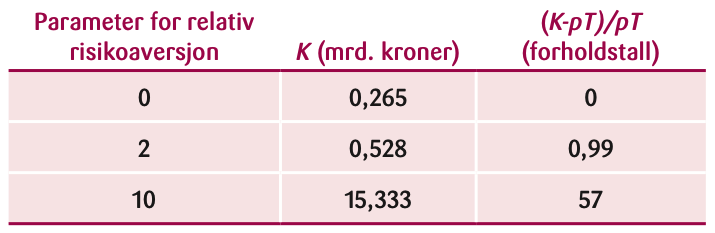
Med risikonøytralitet blir K = pT = 265 millioner kroner. Med en risikoaversjon på 2 finner vi K = 528 millioner kroner og en forsikringspremie på 0,99. I dette tilfellet bør altså samfunnet gjennomføre tiltak som er dobbelt så kostbare som den forventede gevinsten. Det bør likevel ikke avsettes mer enn 528 millioner for å bidra til å forhindre atomkrigen. Resultatet henger sammen med graden av risikoaversjon, men også med at norsk innsats flytter sannsynligheten for atomkrig fra 10/10 000 til 9/10 000, altså ikke veldig mye.
Med en risikoaversjon på 10, som også finner en viss støtte i litteraturen, så stiger forsikringspremien til 57. Da er det ok å avsette drøyt 15 milliarder for å forhindre katastrofen. Det er henimot 20 prosent av forsvarsbudsjettet i 2024.
Det er synd at litteraturen ikke fremviser større grad av enighet om hva den relative risikoaversjonen er, men det er ikke helt urimelig. For eksempel er det mulig at relativ risikoaversjon overfor katastrofer er større enn relativ risikoaversjon overfor dagligdagse hendelser,11 men datagrunnlaget for å måle risikoaversjon overfor katastrofer er dårlig. Alt i alt er det en god ting! Men uten data for risikoaversjonen overfor katastrofer (eller andre viktige data) blir forventet nytte-kriteriet tappet for presisjon. Vi kan si kriteriet er følsomt for verdien på relativ risikoaversjon, og i dette teknokratiske språket ligger det at nytte-kostnadskriteriet kan gi sprikende svar avhengig av hva man antar om en parameter man vet lite om. Det gjør det aktuelt å vurdere andre kriterier.
5. ALTERNATIVER TIL SUBJEKTIVE SANNSYNLIGHETER
5.1. Maxmin og liknende beslutningsregler
Regler som ikke antar noe om sannsynligheter
Dersom en ikke kjenner sannsynligheten p, er det ikke opplagt at en skal akseptere Savage’s forslag om å danne seg subjektive sannsynligheter. Wald (1945) foreslo maxmin-regelen: En skulle velge det alternativet som var best for det verste utfallet. I vårt eksempel fra Tabell 1 er dette ikke-tiltak, da ikke-tiltak i verste fall gir y-T, mens tiltak i verste fall gir y-k-T. En svakhet ved kriteriet er at det gir all vekt til det verst tenkelige utfallet, regelen er uavhengig av q (så sant den er positiv), i tillegg til å være uavhengig av p. Den er også uavhengig av y. Ikke-tiltak blir altså konklusjonen enten en legger en sektor, nasjonen, eller hele verden til grunn i definisjonen av en HILP-hendelse, ja også om man ser på en dagligdags beslutning innenfor vårt problem. Se også Tabell 3. Arrow og Hurwicz (1977) generaliserte maxmin-regelen (med en aksiomatisk begrunnelse) til α-maxmin-regelen: En skal med denne regelen tillegge det verste utfallet en vekt α og det beste utfallet en vekt 1-α. Størrelsen α sier i en viss forstand hvor pessimistisk beslutningstageren er. I vårt eksempel fra Tabell 1 gir ikke-tiltak både høyere verste utfall og beste utfall enn tiltak. Ikke-tiltak er derfor best uansett verdien på vekten α.
Et forslag fra Savage (1954) er minmax-regret-regelen: For hver handling og tilstand kalkulerer man differansen mellom det best mulig oppnåelige og det faktiske utfallet gitt valget. Dette gir en bestemt differanse (regret) for hver tilstand. En ser så på hva den maksimale regret er over tilstander (for hver handling). En velger så den handlingen som gir minst maksimal regret. Med vårt eksempel: For tiltak er max regret lik k (i tilstandene ikke-katastrofe eller katastrofe uansett), mens ikke-tiltak gir max regret lik T-k (i tilstanden katastrofe hvis ikke-tiltak). Hvis k < T-k, dvs. hvis k < T/2, gir derfor tiltak minst max regret, og tiltak bør derfor velges. For HILP-hendelser er T mye større enn realistiske k, slik at dette er den relevante situasjonen: Med T lik 2650 milliarder som over, kan alle tiltak som koster mindre enn 1325 milliarder forsvares.
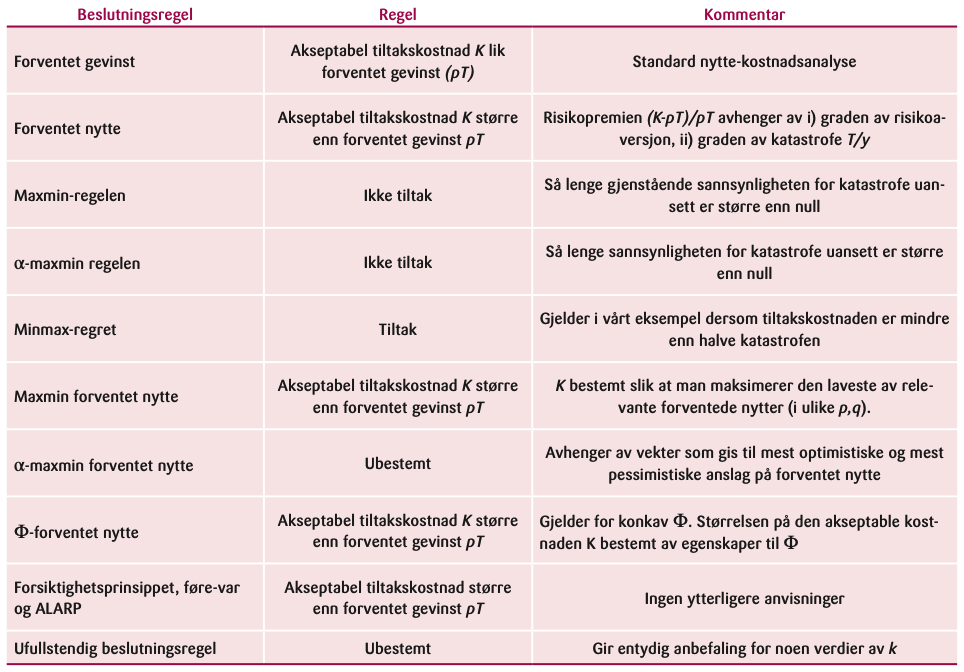
Regelen minmax-regret bryter med aksiomene for teorien bak forventet nytte. I denne teorien antas nytten bare å avhenge av det faktiske utfallet, og ikke av hva vi i ettertid ser at vi kunne oppnådd ved en annen handling. En slik regret-komponent er en følelsesmessig komponent utover det mer snevre fokus på det økonomiske resultatet. Dette kan være rimelig at en slik følelsesmessig komponent blir tatt hensyn til for beslutninger på individ-nivå, men det er langt mer tvilsomt om profesjonelle aktører bør ta hensyn til den.
Regler som antar noe om sannsynligheter
Forslagene over ser helt bort fra hva sannsynligheten er for at en katastrofe skal inntreffe. Selv om vi ikke kjenner denne sannsynligheten med sikkerhet, kan det være rimelig å anta at vi «vet» at sannsynlighetene p og q ligger i intervallene [pL, pH] og [qL, qH]. Med dette utgangspunktet har Gilboa og Schmeidler (1989) foreslått følgende: For hver handling en kan velge, beregnes forventet nytte for alle tenkelige p og q i de aktuelle intervallene. Fra dette finner en den laveste forventede nytten til hver av handlingene. En velger så den handlingen som maksimerer denne laveste forventede nytten. Denne fremgangsmåten kalles maxmin forventet nytte. Hvis vi tenker oss at verdiene på p og q i vårt eksempel over er inneholdt i intervallene, vil nå 528 millioner til 15,3 milliarder utgjøre nedre grenser for K (i det tilfellet at forventet nytte er lavest akkurat ved disse verdiene, som blant annet innebærer at p = pH).
En svakhet med denne fremgangsmåten er at p og q per forutsetning enten ligger eller ikke ligger innenfor et intervall. Ofte vil en tenke at sannsynligheten for p og q er sterkere på noen områder av tallinjen enn andre. Det kan også være en ulempe at nyttefunksjonen tas for gitt når det i praksis er stor usikkerhet om for eksempel risikoaversjon.
Ghiradato mfl. (2004) har generalisert maxmin forventet nytte til α-maxmin forventet nytte. Her beregner en for hver handling både minimum og maksimum forventet nytte, og beregner en veiet sum med hhv. α og 1-α. Dette kriteriet har tilsvarende svakhet som α-maxmin-regelen: I begge tilfeller vil valget mellom handlinger typisk avhenge av verdien på α, og reglene gir ingen rettledning om hvordan denne verdien skal velges. Dessuten vil α-maxmin forventet nytte, som er en generalisering av maxmin forventet nytte, ha de samme svakhetene som sistnevnte.
Mens regelen over bare ser på det mest pessimistiske og det mest optimistiske anslaget på p, antar Klibanoff mfl. (2005) at beslutningstageren har en sannsynlighetsfordeling over alle mulige p i intervallet [pL, pH] (for å forenkle fremstillingen antar vi nå at q er kjent). For hver handling f og hver sannsynlighet p kan en beregne en forventet nytte Esu(f(s);p), hvor f(s) er konsekvensen av handlingen f dersom tilstand s inntreffer. Deretter sammenlignes handlingene ved å beregne en funksjon Φ over disse forventede nyttene, og en velger den handlingen som gir høyest verdi på den forventede verdien av Φ over alle p. En velger med andre ord den handlingen som maksimerer EpΦ(Esu(f(s);p)) hvor f(s) er konsekvensen av handlingen f dersom tilstand s inntreffer.
Dersom Φ er lineær er denne regelen identisk med å velge Ep som den subjektive sannsynligheten. Dersom Φ er konkav (og q = 0) er regelen identisk med å velge en subjektiv p som er høyere enn forventningsverdien Ep. Hvor mye denne subjektive p-verdien avviker fra Ep avhenger blant annet av tapet T. Yttertilfellet med ekstrem konkavitet av funksjonen Φ svarer til maxmin forventet nytte, jf. omtalen av Gilboa og Schmeidler (1989).
Den største svakheten ved denne regelen er at egenskapene til funksjonen Φ kan være viktig for hvilken handling som rangeres høyest, og at det ikke er noen intuitivt opplagt måte å fastlegge denne funksjonen. Regelen vil i praksis si at en justerer de subjektive sannsynligheter i forhold til deres forventningsverdier i retning økt sannsynlighet for dårlige utfall og redusert sannsynlighet for gode utfall. Men nøyaktig hvor mye sannsynlighetene skal justeres avhenger av egenskapene til funksjonen Φ. I vårt enkle eksempel skal p være større jo «mer konkav» funksjonen Φ er.
Beslutningskriterier når q = 0
Til nå har vi sett på en situasjon med tre tilstander: Ingen katastrofe uansett, ingen katastrofe hvis tiltak, katastrofe uansett. Som sagt dekker det en komplisert virkelighet som kan deles i tilstander på ulike måter. For eksempel kan det for enkelte katastrofer være tvil om tilstanden katastrofe uansett. Det kan argumenteres for at det alltid er noe man kan gjøre som vil redusere katastrofen, enten sannsynligheten for den, eller konsekvensen av den. Vi tenker oss nå at sannsynligheten for tilstanden «katastrofe uansett» er null.
Det viser seg at regelen maxmin gir et nytt resultat når vi fjerner tilstanden katastrofe uansett. Tidligere var utfallet y-T-k det dårligste: Vi gjør tiltak, men katastrofen kommer likevel. Det betyr å velge ikke-tiltak. Men om vi fjerner tilstanden katastrofe uansett er det y-T som er det dårligste. Det betyr å velge tiltak. Om man skal velge tiltak eller ikke-tiltak, kommer dermed an på om tilstanden katastrofe uansett er med eller ikke.
Noe av den samme tvetydigheten gjelder α-maxmin. Her fikk vi tidligere ikke-tiltak fordi ikke-tiltak både ga det beste og verste utfallet. Men hvis vi kutter tilstanden katastrofe uansett, gir tiltak det beste av de dårlige utfallene (y-k) og ikke-tiltak det beste av de gode utfallene (y). Når q = 0 vil derfor valget av handling avhenge av størrelsen på α, som regelen ikke sier noe om hvordan en bør fastlegge.
Det virker ikke betryggende at optimal beslutning endrer seg fundamentalt dersom man legger til eller trekker fra en tilstand.
5.2. Verbale beslutningsregler
I samfunnets store samtale om katastrofale eller risikable hendelser bruker man bare delvis de spesifiserte matematiske beslutningsreglene vi har omtalt til nå. I tillegg, og kanskje fortrinnsvis, brukes mer eller mindre presise verbale beslutningsregler. Noen av de viktigste er forsiktighetsprinsippet, føre-var, sikker minimumsstandard og ALARP. Det kan være nyttig å gjennomgå hvilke anvisninger disse reglene gir og hvordan de forholder seg til de matematiske reglene over.
Både forsiktighetsprinsippet og føre-var-prinsippet er definert og drøftet i NOU 2018: 17, vedlegg 1. Her står det:
Forsiktighetsprinsippet er en grunnleggende norm eller regel innen risikostyring som sier at forsiktighet skal være et rådende prinsipp. Tiltak skal iverksettes, eller en skal ikke gjennomføre en aktivitet, når det er usikkerhet knyttet til hva som blir konsekvensene (utfallene) av en aktivitet; med andre ord, når en står overfor risiko.
Det er vanskelig å se at dette er et nyttig begrep i vår sammenheng så lenge det ikke presiseres om alle eller bare noen tiltak skal gjennomføres når en står overfor risiko. Det virker urimelig å gjennomføre alle mulige tiltak. Hvor skal man sette grensen? Prinsippet i seg selv gir ingen anvisning.
Videre står det om føre-var-prinsippet:
Føre-var-prinsippet kan sees på som et underprinsipp av forsiktighetsprinsippet som kommer til anvendelse når en står overfor vitenskapelig usikkerhet (og «ikke bare» risiko). Føre-var-prinsippet uttrykker at tiltak skal iverksettes eller en ikke skal gjennomføre en aktivitet dersom det er betydelig vitenskapelig usikkerhet (uvitenhet) knyttet til konsekvensene av aktivitetene, og disse konsekvensene anses som alvorlige.
Som underprinsipp av forsiktighetsprinsippet gjelder den samme innvendingen her: Hvilke, i universet av mulige tiltak, bør man gjennomføre? Ett ytterpunkt er at tiltakene skal avgrenses av forventet nytte. Et annet er at alle tiltak bør gjennomføres, uansett størrelsen på konsekvensene T, sannsynlighetene p og q, og kostnaden k. I det siste tilfellet minner den om Savages minmax-regret (minus hans tilleggskrav at k ikke kan være større enn halve T).
DFØ (2023) finner kanskje en middelvei når de skriver at «I enkelte analyser kan man ønske å legge inn en ekstra sikkerhetsmargin fordi det er fare for særlig katastrofale og irreversible konsekvenser, selv om sannsynligheten for at disse inntreffer er lav. Dette kalles å følge føre-var-prinsippet.» «En ekstra sikkerhetsmargin» bringer tankene til forsikringspremien vi omtalte tidligere.
I NOU 2012: 16 (kap. 8.4) står det om sikker minimumsstandard at «begrepet er basert på ideen om å minimere det maksimale tap i forbindelse med et prosjekt». Denne definisjonen svarer helt til maxmin-regelen, med svakhetene som omtalt tidligere. NOU 2012: 16 viser også til Bishop (1978), som eksplisitt ser på at gevinsten pT (i vår terminologi) er ukjent. Dermed kan ikke den maksimale kostnaden K beregnes, og Bishop foreslår i stedet å sette K skjønnsmessig. Dette innebærer i så fall at en gir opp å gjennomføre en analyse som kan hjelpe oss til å fastslå K. Prinsippet er derfor ikke særlig nyttig når det gjelder å vurdere tiltak som kan redusere risikoen for store tap.
Et prinsipp for å analysere risikoreduserende tiltak har navnet ALARP. Dette forklares slik på Wikipedia per januar 2024:
ALARP («as low as reasonably practicable»), or ALARA («as low as reasonably achievable»), is a principle in the regulation and management of safety-critical and safety-involved systems (…) For a risk to be ALARP, it must be possible to demonstrate that the cost involved in reducing the risk further would be grossly disproportionate to the benefit gained.
I vårt tilfelle er det mulig å redusere risikoen for katastrofe fra q+p til q ved å velge tiltak, som derfor ifølge ALARP bør velges dersom dette er praktisk mulig («reasonably practicable») og kostnaden ikke er urimelig overdreven («grossly disproportionate») i forhold til gevinsten. Det er uklart hva som menes med disse begrepene. I Preventor (2006) står det:
«ALARP-prinsippet innebærer… at identifiserte tiltak skal implementeres, med mindre det kan dokumenteres at det er et urimelig misforhold mellom kostnader/ulemper og nytte.»
Petroleumstilsynet (2017) skriver:
«Ved reduksjon av risiko skal den ansvarlige velge de tekniske, operasjonelle eller organisatoriske løsningene som etter en enkeltvis og samlet vurdering av skadepotensialet og nåværende og framtidig bruk gir de beste resultater, så sant kostnadene ikke står i et vesentlig misforhold til den risikoreduksjonen som oppnås.»
Det er ikke opplagt hvordan en bør presisere «grossly disproportionate» (As low as reasonably practicable, 2024) eller «vesentlig misforhold» (Rammeforskriften (petroleumsvirksomheten), § 11). En tolkning er at hvis kunnskapene om konsekvensen av katastrofen (T) og sannsynlighetsreduksjonen et tiltak kan oppnå (p) er mangelfull, bør en ta utgangspunkt i de høyest tenkelige verdiene og sette K = (pT)max.
Enkelte hevder at forventningsverdier av typen pT er av begrenset relevans når en skal vurdere tiltak som reduserer små sannsynligheter for alvorlige negative hendelser. I forbindelse med mulige ulykker i petroleumssektoren skriver for eksempel Abrahamsen mfl. (2016):
«Det å bruke nytte-kostnadsanalyser som grunnlag for regelverksendringer i petroleumsvirksomheten bryter med forsiktighetsprinsippet, et prinsipp som på mange måter kan sies å være selve fundamentet for risikostyringen og sikkerhetstenkningen i bransjen. Forsiktighetsprinsippet innebærer at forsiktighet skal være et styrende prinsipp der det knyttes usikkerhet til hva som blir konsekvensene.»
Etter en påpeking om at (i vår terminologi) T kan være mye større enn pT konkluderer Abrahamsen mfl. (2016) som følger:
«Det vi trenger er analyser og evalueringer av antatte konsekvenser, kostnader og nyttegevinster som evalueres i en mye bredere kontekst enn hva tilfellet er gjennom tradisjonelle nytte-kostnadsanalyser. For å ta gode beslutninger når det gjelder sikkerhet, må risiko og usikkerhet vektlegges – forventningsverdier gir ikke et egnet underlag. Først da vil vi kunne oppnå kostnadseffektiv regulering av storulykkesrisiko i petroleumsindustrien. Hvis man likevel velger å ta beslutninger basert på nytte-kostnadsanalyser, så vil man raskt kunne ende opp med både høyere storulykkesrisiko, og reguleringer som er alt annet enn kostnadseffektive.»
Utover å oppfordre til å legge høy vekt på gevinsten av tiltak (pT i vår terminologi) og liten vekt på kostnad, har vi vanskelig for å se hvordan denne konklusjonen i praksis skal hjelpe oss i avveininger mellom sannsynlighetsreduksjoner og tiltakskostnader. I denne situasjonen kan et alternativ være å se hvordan ulike etater i praksis tolker et føre-var-prinsipp, for eksempel hvor stor forsikringspremie mellom forventet gevinst (pT i vår terminologi) og kostnad (k) som aksepteres (ev. hvilken relativ risikoaversjon man legger til grunn). Dette er vanskelig i praksis, fordi mange etater i dag kun har en overordnet oppfatning av pT og k for tiltak de innfører. Uansett gir det ingen prinsipiell støtte, bare en indikasjon på hva som gjøres andre steder. Selv det å vite hva man gjør andre steder gir ikke nødvendigvis så mye hjelp uten tilleggsforutsetninger: Som presisert tidligere peker kriteriet forventet nytte på at man bør se forholdet mellom pT og k i sammenheng med inntekt og formue (y), og i sammenheng med hvilken restrisiko som foreligger (q). Det kan kanskje antas at ulike etater forholder seg til samme y, nemlig BNP eller nasjonalinntekten, men det er heroisk å anta at de forholder seg til samme q.
5.3. Ufullstendige beslutningsregler
Beslutningsreglene drøftet til nå har som formål å gi en presis anbefaling om hvordan en beslutningstager skal velge mellom to handlinger. Baldwin (2018) og Danan mfl. (2016) ser på situasjoner hvor slike presise anbefalinger ikke alltid er mulig. Poenget belyses enklest med en samfunnsøkonomisk analyse (med risikonøytralitet) hvor alle ingredienser i analysen er kjent unntatt sannsynlighetsreduksjonen p. I mange tilfeller vil beslutningstageren likevel føle seg trygg på at sannsynligheten p ligger i et intervall [pL, pH], men ikke ha noen formening om sannsynligheten utover dette. Vi kjenner igjen dette fra reglene maxmin forventet nytte og α-maxmin forventet nytte tidligere i artikkelen. For situasjonen i Tabell 1 vil det da være en entydig anbefaling om å velge tiltak dersom k < pLT og å velge ikke-tiltak dersom k > pHT. Dersom pLT < k < pHT finnes det ingen entydig anbefaling. Både tiltak og ikke-tiltak kan i dette tilfellet forsvares (justifiable acts i terminologien til Baldwin (2018)).
Resonnementet over kan utvides til ufullstendig informasjon ikke bare om p, men også om q og T, og egenskaper ved preferansene. Eksempel på sistnevnte er at de involverte i beslutningen er sikre på at relativ risikoaversjon ligger mellom 2 og 10. Fra våre tidligere resultater kan vi da slå fast at vi bør entydig anbefale tiltak dersom kostnaden k er lavere enn 528 millioner og entydig anbefale ikke-tiltak dersom kostnaden er høyere enn 15,3 milliarder. For verdier av k mellom 528 millioner og 15,3 milliarder kan en forsvare både tiltak og ikke-tiltak.
6. AVSLUTNING
Bak en ufullstendig beslutningsregel som denne ligger det en erkjennelse av at selv om økonomisk analyse kan hjelpe oss et stykke på vei i en beslutning ved å snevre inn hva som er fornuftig, blir beslutningen til slutt en skjønnsmessig avgjørelse innenfor det innsnevrede mulighetsområdet. For Pascal var saken klar, han forlot en strålende karriere som matematiker og fysiker og viet sitt liv til religionen.
Referanser:
Abrahamsen, E. B., T. Aven og T. Husebø (2016). Må ta mer hensyn til risiko og usikkerhet i oljebransjen. Forskning.no. Tilgjengelig fra: http://forskning.no/meninger/kronikk/2016/10/mer-hensyn-til-risiko-usikkerhet-oljebransjen
As low as reasonably practicable (2024) i Wikipedia. Tilgjengelig fra: https://en.wikipedia.org/wiki/As_low_as_reasonably_practicable (hentet januar 2024).
Arrow, K. og L. Hurwicz (1977). Appendix: An optimality criterion for decision-making under ignorance, i Studies in resource allocation processes. Cambridge University Press, Cambridge, s. 461–472.
Baldwin, E. (2018). Choosing in the dark: incomplete preferences, and climate policy. Arbeidsnotat. Tilgjengelig fra: http://elizabeth-baldwin.me.uk/papers/choosingDark.pdf
Dalen, H. M. og B. Halvorsen (2022). Økonomiske konsekvenser av høye kraftpriser og strømstønad. Rapporter 2022/36, Statistisk sentralbyrå.
Danan, E., T. Gajdos, B. Hill og J.-M. Tallon (2016). Robust social decisions. American Economic Review 106, 2407–2425.
DFØ (2023). Veileder i samfunnsøkonomiske analyser. Direktoratet for økonomistyring. Tilgjengelig fra: https://dfo.no/fagomrader/utredning-og-analyse-av-statlige-tiltak/samfunnsokonomiske-analyser/veileder-i-samfunnsokonomiske-analyser
Doorman, G., K. Uhlen, G. Kjølle og E. S. Huse (2006). Vulnerability analysis of the Nordic power system. IEEE Transactions on Power Systems 21, 402–410. Tilgjengelig fra: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1708873
Elminejad A., T. Havranek og Z. Irsova (2022). Relative risk aversion: A meta analysis. Arbeidsnotat, Charles University, Praha.
Finansdepartementet (2021). Prinsipper og krav ved utarbeidelse av samfunnsøkonomiske analyser mv. Rundskriv R-109/21. Tilgjengelig fra: https://www.regjeringen.no/globalassets/upload/fin/vedlegg/okstyring/rundskriv/faste/r_109_2014.pdf
Gandelman, N. og R. Hernández-Murillo (2015). Risk aversion at the country level. Federal Reserve Bank of St. Louis Review 97 (1), 53–66.
Ghirardato, P., F. Maccherone og M. Marinacci (2004). Differentiating ambiguity and ambiguity attitude. Journal of Economic Theory 118, 133–173.
Gilboa, I., og D. Schmeidler (1989). Maxmin expected utility with non-unique prior. Journal of Mathematical Economics 18 (2), 141–153.
Heal G. og A. Millner (2013). Uncertainty and Decision Making in Climate Change Economics. Review of Environmental Economics and Policy 8, 120–137.
Klibanoff, P., M. Marinaci og S. Mukerji (2005). A smooth model of decision making under ambiguity. Econometrica73 (6), 1849–1892.
Lønning, P. (1980). Et veddemål. Universitetsforlaget.
NOU 2012: 16. Samfunnsøkonomiske analyser.
NOU 2018: 17. Klimarisiko og norsk økonomi.
NVE (2023). Strømbrudd: rettigheter og regler. Tilgjengelig fra: https://www.nve.no/reguleringsmyndigheten/kunde/nett/stroembrudd-rettigheter-og-regler/
Posner, R. A. (2004). Catastrophe: risk and response. Oxford University Press.
Preventor (2006). ALARP-prosesser. Utredning for Petroleumstilsynet. Tilgjengelig fra: http://www.ptil.no/getfile.php/z%20Konvertert/Helse%2C%20milj%C3%B8%20og%20sikkerhet/Sikkerhet%20og%20arbeidsmilj%C3%B8/Dokumenter/alarpprosesserendelig.pdf
Rammeforskriften (petroleumsvirksomheten). Forskrift om helse, miljø og sikkerhet i petroleumsvirksomheten og på enkelte landanlegg (rammeforskriften). Tilgjengelig fra: https://lovdata.no/dokument/SF/forskrift/2010-02-12-158
Savage, L. J. (1954). The foundations of statistics. Wiley and Sons.
Sintef (2016). HILP – analyse av ekstraordinære hendelser i kraftsystemet. Tilgjengelig fra: https://www.sintef.no/prosjekter/2016/hilp/
Taleb, N. N. (2007). The black swan: The impact of the highly improbable. Random House.
Hoel M. og H. Vennemo (2018). Økonomisk analyse av HILP-hendelser. Rapport nr. 31/2018, Vista Analyse.
Hoel M. (2021). Klimarisiko og kostnads-nytteanalyse. Rapport nr. 27/2021, Vista Analyse.
Wald, A. (1945). Statistical decision functions which minimize the maximum risk. The Annals of Mathematics 46 (2), 265–280.
Weitzman, M. L. (2011). Fat-tailed uncertainty in the economics of catastrophic climate change. Review of Environmental Economics and Policy 5 (2), 275–292.
Fotnoter:
- Takk til en anonym fagfelle og tidsskriftets redaktør Lars-Erik Borge for gode kommentarer til et utkast. ↩︎
- Deler av dette arbeidet bygger også i noen grad på Heal og Millner (2013). ↩︎
- Strømbruddet i eksempelet og alvorligere strømbrudd er omtalt som «catastrophic» i Doorman mfl. (2006) ↩︎
- Respondentene i Vista Analyse (2018) sin representative, lands- omfattende undersøkelse har til sammenlikning en gjennomsnittlig betalingsvillighet for å unngå 24 timers strømbrudd på 1000 kroner. Faktisk kompensasjon for å unngå et strømbrudd inntil 24 timer var i januar 2024 980 kroner (NVE, 2023). Dette er tall langt under 10.000 kroner. Samtidig er det i eksemplet sett bort fra at et strømbrudd vil ramme også næringsliv og andre etater. ↩︎
- Verdien av oljefondet, per 19. januar 2024, var ca. 16.000 milliarder kroner. ↩︎
- https://no.wikipedia.org/wiki/Klimasjokket_i_535%E2%80%93536 ↩︎
- Et banalt eksempel er at en normalfordeling med estimert varians ut- gjør en t-fordeling. ↩︎
- Hvordan en slik nyttefunksjon for samfunnet eventuelt kan avledes av innbyggernes risikopreferanser ligger utenfor problemstillingene i denne artikkelen. ↩︎
- Den første ulikheten kan bli reversert hvis q er stor positiv. Tolkningen er at det etter tiltaket fortsatt er såpass stor risiko for katastrofe at en ikke ønsker en stor tiltakskostnad i tillegg til tapet fra katastrofen i dette tilfellet. Vi bruker ikke mer plass på denne muligheten. ↩︎
- Dersom r=1 er i stedet u(x)=Lnx. Uansett verdien på r har vi at u’=x-^r. ↩︎
- Det sier seg selv at den da ikke lenger er konstant. ↩︎

