Fallgruver i frontfagets hovedkursteori¹

1. INTRODUKSJON

Hovedkursteorien i Aukrust (1977) har vært og er sentral for lønnsfastsettelsen i Norge. Frontfagsmodellen beskriver forhandlingsstrukturen i de norske lønnsforhandlingene. Hovedkursteorien benyttes som retningslinje for hvordan lønningene bør fastsettes på lang sikt i disse forhandlingene. Teoriens hovedbudskap er at k-sektor bør være lønnsledende ved at lønnsveksten i k-sektor danner rammen for resten av økonomien, samt at lønna i k-sektor bør bestemmes av lønnsevnen til industrien. Modelleringen av lønnstilpasningen på lang sikt, som er basert på antakelsen om en konstant fordeling av faktorinntekt til arbeidere og kapitaleiere, er imidlertid mangelfull. Investorers avkastningskrav inngår ikke eksplisitt i bestemmelsen av lønnsnivået på lang sikt i Aukrust-modellen. Man kan derfor ikke være sikker på om investeringer i k-sektor blir lønnsomme på lang sikt. Denne egenskapen ved Aukrust-modellen er omtalt i Rødseth (2000), NOU 2013: 13 og NOU 2023: 30, som også påpeker at det avgjørende kriteriet for at k-sektor kan opprettholdes på sikt er at slike investeringer gir en normal avkastning.² Lønnsandelen vil ifølge NOU 2023: 30 kunne endres av strukturelle årsaker som sammensetningseffekter eller teknologiske endringer. NOU 2023: 30 viser videre til Bjørnstad og Nymoen (1999), som finner at lønnsandelen er et godt mål på kapitalrentabilitet i norsk industri. Både NOU 2023: 30 og NOU 2025: 4, Grunnlaget for inntektsoppgjøret 2025, legger til grunn at en stabil lønnsandel også indikerer stabil lønnsomhet. Men er dette premisset relevant i tiden framover, og hva blir konsekvensene for lønnsfastsettelsen om premisset videre-føres?

Denne artikkelen bidrar til litteraturen ved å analysere hvordan lønnsfastsettelsen kan påvirkes av substitusjonsmulighetene mellom arbeid og kapital i tiden framover. Artikkelen avdekke at praksisen med å tilpasse lønnssatsen slik at man styrer mot en konstant lønnskostnadsandel på lang sikt i enkelte tilfeller vil føre til en lønns- og lønnskostnadsandelsspiral som gjør investeringer i k-sektor ulønnsomme. Analysen viser at et slikt destabiliserende utfall inntreffer når substitusjonselastisiteten mellom arbeid og kapital er høyere enn 1. Ny empiri finner nettopp at substitusjonselastisiteten i k-sektor er vesentlig høyere enn 1, og betydelig høyere enn tidligere anslag, se Von Brasch mfl. (2024). Planlagte lanseringer av menneskeliknende roboter basert på AI-teknologi vil trolig utvide substitusjonsmulighetene. Slike teknologiskift kan også føre til mer momentane fall i lønnskostnadsandelen. Spiralen oppstår fordi økt lønnssats som følge av lav initial lønnskostnadsandel isolert sett fører til høyere lønnskostnadsandel og lavere lønnsomhet. Høyere lønnssats og lavere lønnsomhet gir insentiver til å substituere arbeidskraft med kapital, noe som isolert sett reduserer lønnskostnadsandelen. Hvis substitusjonselastisiteten mellom arbeid og kapital er større enn 1 dominerer den siste effekten over den første. Dermed faller lønnskostnadsandelen som følge av høyere lønnssats. Økt lønnssats for å sikre “sin del av kaka” kan dermed utløse en spiral som undergraver lønnsomheten i k-sektor. Hvis substitusjonselastisiteten er lik 1 er lønnskostnadsandelen upåvirket på tross av redusert lønnsomhet. Lønnsomheten i k-sektor er derfor truet også i dette tilfellet. Disse utfallene kan imidlertid unngås dersom partene i arbeidslivet legger til grunn at en stabil fordeling av verdiskapingen ikke nødvendigvis innebærer stabil lønnsomhet i k-sektor.

Rødseth (2000) sammenlikner hovedkursteorien med modellen i Kouri (1979), der lønnssatsen og lønnskostnadsandelen bestemmes av avkastningskravet i k-sektor. Hvis lønnssatsen settes slik at avkastningskravet innfris, og realisert lønnskostnadsandel samtidig er lik den andelen partene i arbeidslivet oppfatter som normalandelen, vil lønnsfastsettelse basert på hovedkursteorien bli identisk med lønnsfastsettelse basert på et avkastningskrav ifølge Rødseth (2000). Disse innsiktene er forenlig med modellegenskapene i denne artikkelen. Rødseth (2000) påviser også at lønnskostnadsandelen faller når avkastningskravet øker og substitusjonselastisiteten er lavere enn 1 (og motsatt). Hovedkursteorien overdriver derfor rommet for lønnsvekst i perioder med økende rente ifølge Rødseth (2000), noe som også er forenlig med modellegenskapene i denne artikkelen. Det finnes imidlertid ingen beskrivelser av lønns- og lønnskostnadsandelsspiraler forbundet med praktiseringen av hovedkursteorien i Rødseth (2000) eller de andre omtalte studiene.

Lønnskostnadsandelen i industrien i Norge har vært forholdsvis stabil de siste tiårene, se figur 4.22 i Bjertnæs mfl. (2023).³ Avkastningen har også vært forholdsvis stabil når man justerer for konjunktursituasjonen, se figur 4.13 i Konjunkturtendensene (2021). Eldre empiriske studier finner dessuten at substitusjonselastisiteten er lavere enn 1, se diskusjon i Acemoglu (2003) og Von Brasch mfl. (2024). I slike tilfeller fører økt lønnssats til økt lønnskostnadsandel, og man unngår en destabiliserende spiral. En lønnsfastsettelse med mål om stabil lønnskostnadsandel er forenlig med stabil lønnsomhet i slike tilfeller. De lavere anslagene i eldre studier gir derfor en forklaring på hvorfor vi ikke har observert destabiliserende spiraler tidligere. Merk også at realkapitalen i stor grad er gitt på kort sikt siden det ofte er tidkrevende og kostbart å endre realkapitalbeholdningen i K-sektor. Substitusjonsmulighetene mellom arbeid og kapital vil da være begrenset. Man unngår dermed destabiliserende lønns- og lønnskostnadsandelsspiraler. På kort sikt vil dessuten lønnsfastsettelsen være preget av det makroøkonomiske konjunkturbildet, se Bjertnæs mfl. (2023). Et mål om stabile faktorinntektsandeler i lønnsfastsettelsen vil derfor spille en annen rolle på kort sikt. Formålet med denne artikkelen er imidlertid å belyse forhold ved lønnsfastsettelsen på lang sikt.

Artikkelen bidrar også til litteraturen ved å påvise at det er feil at lønnssatsen må vokse i takt med produktivitetsveksten i k-sektor når produktprisen holdes konstant, slik Aukrust-modellen impliserer og NOU 2013: 13 og NOU 2023: 30 påpeker. Lønnssatsen må vokse raskere enn total faktorproduktivitet siden avkastning per kapitalenhet ikke endres og den økte verdiskapingen som følger av vekst i total faktorproduktivitet skal deles mellom arbeidere og kapitaleiere. Det er også feil å anta at lønnskostnadsandelen må være konstant i dette tilfellet. Når lønnssatsen settes slik at et avkastningskrav innfris blir lønnskostnadsandelen konstant, voksende eller fallende hvis substitusjonselastisiteten mellom arbeid og kapital er lik, lavere eller større enn 1. Inflasjonsprediksjonene i Aukrust-modellen er altså ikke forenlig med prediksjoner som tar hensyn til at investorer har et avkastningskrav. I de senere årene har priser på varer i k-sektor økt i kombinasjon med at kursen på norsk valuta har svekket seg. Analysen viser at slik prisvekst i k-sektor vil slå ut i en tilsvarende lønnsvekst på lang sikt. Dette resultatet er identisk med resultatet i Aukrust-modellen.

2. MODELLEN

Artikkelen tar utgangspunkt i Aukrust-modellens beskrivelse av lønnsfastsettelsen i Norge, der k-sektor er lønnsledende. Antagelsen om at normal avkastning på kapital sikres av en antagelse om konstante faktorinntektsandeler erstattes her av et eksplisitt avkastningskrav basert på optimerende investoratferd. Denne modifikasjonen sikrer at investeringer i k-sektor blir lønnsomme ved at avkastningskravet må innfris på lang sikt. Modellen tallfestes basert på k-sektoren i den makroøkonomiske modellen KVARTS, siden KVARTS blant annet benyttes av Teknisk beregningsutvalg i forkant av lønnsforhandlinger for å beregne prisvekst. Modelleringen er forenlig med argumentasjonen i Aukrust (1977) om at et normalavkastningsnivå for kapitalen skal innfris på lang sikt. Aukrust-modellen inneholder som nevnt ikke et slikt avkastningskrav.

Det antas at produksjonsteknologien er identisk med produksjonsteknologien i KVARTS og NORA modellene. Det antas altså at produksjonen, ​X​, er gitt ved følgende CES-produktfunksjon:

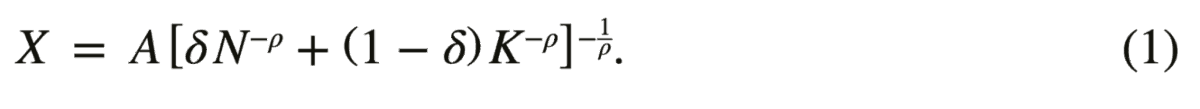
Her angir ​K​ realkapitalbeholdning og ​N​ timeverk. Produktiviteten måles som total faktorproduktivitet, A, på samme måte som i KVARTS og NORA. Det antas videre at bedriftene i k-sektor maksimerer sin profitt, ​π​, for gitt lønnssats, W, produktpris, ​​P​ _T​​​ , og avkastningskrav, ​​P​ _K​​​.

Profittmaksimerende atferd kombinert med produktfunksjonens egenskaper og fri etablering gir følgende førsteordenbetingelser:

Og

Lønnskostnadsandelen, ​L​, er definert som

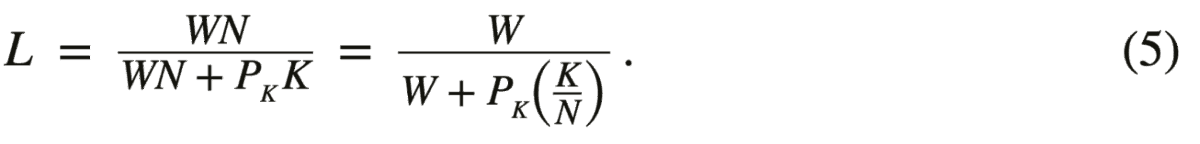
Likning (3), (4) og (5) beskriver lønnsfastsettelsen på lang sikt når man tar hensyn til at investorer har et normalavkastningskrav. Likning (3) bestemmer da mengden kapital per arbeider, ​​ ^K _ _N ​​ , for gitt avkastningskrav, ​​P​ _K​​​. Likning (4) bestemmer lønnssatsen, W, for gitt mengde kapital per arbeider, ​​ ^K _ _N ​​. Lønnssatsen blir dermed bestemt av avkastningskravet. En høyere lønnssats ville gitt en avkastning som var lavere enn avkastningskravet, og en lavere lønnssats ville gitt en avkastning som var høyere enn avkastningskravet. I den førstnevnte situasjonen blir investeringer ulønnsomme, mens renprofitt oppstår i den sistnevnte situasjonen. Slike situasjoner er vanlige på kort- og mellomlang sikt. Korrigerende mekanismer vil imidlertid trekke lønnssatsen mot en løsning med normalavkastning på lang sikt ifølge Aukrust (1977).

Likning (5) bestemmer lønnskostnadsandelen, ​L​, for gitt avkastningskrav, ​​P_{​ K​​​}, lønnssats, W, og mengde kapital per arbeider, ​​ ^K _ _N ​​. Merk at både lønnssats og lønnskostnadsandel bestemmes uten at selve nivået på kapitalen og arbeidskraften er fastlagt. Det er tilstrekkelig at kapitalintensiteten, dvs. kapital per arbeider, blir bestemt av avkastningskravet. Denne modellegenskapen følger av antagelsen om konstant skalautbytte i produksjonen.

Det er altså produktprisen, produktiviteten, produktfunksjonens egenskaper og avkastningskravet som bestemmer lønnssatsen med en slik lønnsfastsetting. Om det er hensiktsmessig å anta en konstant fordeling av faktorinntekt mellom arbeid og kapital, for deretter å benytte avvik fra en slik fordeling som indikator på om lønnsfastsettelsen sikrer en normal avkasting på kapital, er ikke opplagt. Artikkelen analyserer dette spørsmålet i avsnittene nedenfor vha. modellsimuleringer. Artikkelen studerer også effektene av økonomisk vekst og endringer i priser når lønnsfastsettelsen bestemmes av modellen ovenfor. Resul-tatene sammenliknes med resultater fra Aukrust-modellen for å avdekke forskjeller.

Det innføres to ekstra likninger for å kunne tallfeste endringer av økonomiske variabler på en enkel måte. Artikkelen antar at avkastningskravet per enhet realkapital, ​​P​ _K​​​, er lik avkastningskravet per krone investert, ​r​, multiplisert med pris per kapitalenhet, som antas å være lik produktprisen i k-sektor, ​​P​ _T​​​. En slik tilnærming er relevant når investeringsvarer også er k-sektor varer. Det finnes imidlertid mange forskjellige k-sektorvarer med ulik prisutvikling. Enkelte investeringsvarer, som bygningskapital, inngår dessuten ikke i k-sektor. Det kreves en litt annen tilnærming i slike tilfeller.

Artikkelen antar også at mengden arbeidskraft, ​​^_ N​​, er gitt, samt at arbeidskraften fordeles mellom k-sektor, ​N​, og en skjermet sektor som inkluderer offentlig sektor, ​​N​ _s​​​. Det antas at arbeidskraften i skjermet sektor er gitt.

De fem likningen (3)-(7) bestemmer de fem endogene variablene ​N, K, ​P​ _K​​, W​ og ​L​. Siden både total arbeidskraft og arbeidskraft i skjermet sektor er gitt, blir arbeidskraft i k-sektor bestemt av likning (7). Kapitalmengden per arbeider bestemmes av avkastningskravet i likning (3). Likning (3) bestemmer derfor kapitalmengden, ​K​, for en gitt mengde arbeidskraft, ​N​. Lønnssatsen bestemmes som nevnt av kapitalmengden per arbeider i likning (4). Denne enkle modellen kan løses analytisk. En tallfesting er imidlertid mer hensiktsmessig og informativ for å belyse svakheter ved lønnsfastsettelsen i Norge på lang sikt.

1.1. Tallfesting av modellen

Den enkle modellen ovenfor kalibreres slik at modellen gjenskaper tallgrunnlaget for 2024 for avlønning av arbeidskraft, kapital samt verdiskaping i k-sektor i KVARTS.⁴ KVARTS er igjen kalibrert mot industrien i nasjonalregnskapet. Merk også at k-sektor i KVARTS består av tre sektorer. Kalibreringen til en k-sektor innebærer at analysen utelater sammensetningseffekter mellom næringer.

Faktorinntekten som tilfaller arbeidskraften settes lik lønnskostnadsandelen i den aggregerte k-sektoren multiplisert med total faktorinntekt som fordeles mellom arbeidere og kapitaleiere. Avkastningskravet og kapitalbeholdningen er beregnet slik at det resterende av faktorinntekten tilfaller kapitaleierne. Kapitalslit og sektorskatter er utelatt. Avkastningskravet er basert på observert avkastning som tilfaller kapitaleierne i k-sektor, samt utledet avkastningskrav i Bjertnæs (2023). Historisk sett har avkastningen ved å investere i aksjer vært høyere enn ved plasseringer i bank. Profitt forbundet med patenter, merkevarer, risiko og markedsmakt vil dessuten inngå i faktorinntekten som tilfaller kapitaleierne. Det er rimelig å anta at investeringsselskaper som eier patenter og merkevarer vil kreve en ekstra avkastning som reflekterer verdien av sin markedsmakt. I modellrammeverket er avkastningskravet tilpasset for å ta hensyn til denne informasjonen. Avkastningskravet overstiger derfor markedsrenta på bankinnskudd. Tall-fest-in-gen gir følgende verdier:

Tabell 1. Økonomiske variable, k-sektor 2024.

I hovedscenarioet, Scenario A, er substitusjonsparameteren ​ρ​ satt lik 0,1765 slik at substitusjonselastisiteten mellom kapital og arbeidskraft er lik 0,85, som i KVARTS. Flere studier finner enda lavere anslag på substitusjonselastisiteten, se oversikten i Acemoglu (2003). I Scenario B er substitusjonsparameteren ​ρ​ satt lik -0,4 slik at substitusjonselastisiteten er lik 1,66, noe lavere enn anslaget i Von Brasch mfl. (2024) på 1,9, som finner at tidligere studier undervurderer nivået på denne elastisiteten. Scenario B er i så fall relevant i tiden framover.

3. LØNNSFASTSETTELSE BASERT PÅ HOVEDKURSTEORIEN

NOU 2023: 30 og NOU 2025: 4 legger som nevnt til grunn at en stabil lønnskostnadsandel i K-sektor også indikerer at lønnsomheten er stabil. Hovedkursteorien praktiseres derfor slik at lønnsveksten justeres dersom lønnskostnadsandelen avviker fra et normalnivå. En observert lønnskostnadsandel høyere enn andelen partene i arbeidslivet oppfatter som normalandelen tolkes som et signal om at lønnsveksten må reduseres. En observert lønnskostnadsandel lavere enn normalen tolkes som et signal om at lønnsveksten kan økes. Dette avsnittet analyserer om en slik praktisering av lønnsfastsettelsen realiserer et lønnsnivå som sikrer at avkastningskravet innfris i k-sektor. Artikkelen studere også om en slik lønnsfastsettelse er stabiliserende i den forstand at avvik fra normalnivået for lønnskostnadsandelen utløser lønnstilpasninger som sikrer at kapitalavkastningskravet innfris i k-sektor på lang sikt.

Modellteknisk endres den enkle modellen ovenfor ved å anta at lønnssatsen settes basert på nivået på lønnskostnadsandelen. Denne lønnssatsen bestemmer faktorforholdet i likning (4), og faktorforholdet bestemmer kapitalavkastningen i likning (3). Kapitalavkastningen blir altså endogent bestemt i en slik løsning. I likning (5) bestemmer lønnssats, kapitalavkastning og faktorforhold realisert lønnskostnadsandel. Hvis lønnssatsen settes slik at avkastningskravet innfris, og initial samt realisert lønnskostnadsandel samtidig er lik den andelen partene i arbeidslivet oppfatter som normalandelen, vil lønnsfastsettelse basert på hovedkursteorien bli identisk med lønnsfastsettelse basert på et eksplisitt avkastningskrav. Hvis realisert kapitalavkastning derimot blir lavere enn avkastningskravet, vil hovedkursteorien overdrive rommet for lønnsvekst, se også Rødseth (2000).

1.2. Hovedkursteoriens stabiliserende egenskaper

Artikkelen analyserer om lønnsfastsettelse basert på hovedkursteorien er stabiliserende i situasjoner der initial lønnskostnadsandel avviker fra et normalnivå. Det antas en initial tilstand der lønnskostnadsandel er lavere enn normalnivået, og at lønnssatsen øker som følge av den lave lønnskostnadsandelen. Artikkelen studerer deretter hvordan denne lønnsøkningen påvirker lønnskostnadsandelen og kapitalavkastningen i den langsiktige løsningen.

Økt lønnssats innebære i første omgang at avkastning per kapitalenhet reduseres. I modellsimuleringer der produktivitetsveksten er satt lik null økes lønnssatsen slik at avkastning per krone investert reduseres fra 8 til 5 prosent. Modellsimuleringer viser at lønnssats per timeverk øker fra 459 kroner til 519 kroner i Scenario A, og til 538 kroner i Scenario B. Lønnssatsen økes mer i scenario B siden bedriftene i større grad kan substituere seg bort fra den dyrere arbeidskraften.

Modellsimuleringene viser også at størrelsen på substitusjonselastisiteten mellom kapital og arbeidskraft er avgjørende for effekten på lønnskostnadsandelen. Dette følger som nevnt av likning (5). Antar man en substitusjonselastisitet lik 0,85, som i Scenario A, øker lønnskostnadsandelen fra 0,785 til om lag 0,8 som følge av høyere lønnssats og lavere avkastning. Det er altså en positiv sammenheng mellom lønnssats og lønnskostnadsandel i dette tilfellet, fordi substitusjonselastisiteten er mindre enn 1. En lønnskostnadsandel lavere enn normalen gir lønnsvekst som øker lønnskostnadsandelen. En lønnskostnadsandel høyere enn normalen gir lavere lønnsvekst og lavere lønnskostnadsandel. Lønnssatsen justeres på denne måten mot et nivå som gir et normalt nivå på lønnskostnadsandelen. Er denne lønnssatsen tilpasset slik at kapitalavkastningen blir lik avkastningskravet, realiseres som nevnt løsningen i avsnitt 2, der et gitt avkastningskrav bestemmer lønnssatsen.

I Scenario B, der substitusjonselastisiteten er satt lik 1,66, blir imidlertid utfallet et annet. I Scenario B faller lønnskostnadsandelen fra 0,785 til 0,706 som følge av høyere lønnssats og lavere avkastning. Forklaringen er at høyere lønnssats og lavere avkastning isolert sett øker lønnskostnadsandelen. Høyere lønnssats og lavere avkastning fører imidlertid også til substitusjon mot en løsning med mer kapital per arbeider, noe som isolert sett reduserer lønnskostnadsandelen. Når substitusjonselastisiteten er større enn 1 dominerer den siste effekten over den første. Det er altså en negativ sammenheng mellom lønnssats og lønnskostnadsandel. En lønnskostnadsandel lavere enn normalen gir lønnsvekst som fører til et fall i lønnskostnadsandelen. Fallet i lønnskostnadsandelen gir et forsterket signal om lønnsvekst, som igjen vil redusere lønnskostnadsandelen ytterligere. Praktiseringen av hovedkursteorien, som legger til grunn at stabil lønnskostnadsandel innebærer stabil lønnsomhet, fører altså til en lønns- og lønnskostnadsandelsspiral som innebærer at investeringer i k-sektor blir ulønnsomme i dette tilfellet. Å benytte observerte lønnskostnadsandeler for å fastsette lønnssatsen, slik hovedkursteorien praktiseres, vil i slike tilfeller være destabiliserende og destruktivt for norsk økonomi. Denne praktiseringen av hovedkursteorien blir altså til en fallgruve i dette tilfelle.

I tilfelle med en substitusjonselastisitet mellom arbeidskraft og kapital (tilnærmet) lik 1, blir realisert lønnskostnadsandel ikke påvirket av en økning i lønnssatsen. Hvis partene i arbeidslivet mener at observert lønnskostnadsandel er lavere enn normalen i dette tilfellet, og krever lønnsvekst, vil partene ikke få signaler i form av endret lønnskostnadsandel. Man risikerer da videre lønnsvekst som innebærer at investeringer i k-sektor blir ulønnsomme. Er lønnsveksten isteden tilpasset avkastningskravet, realiseres løsningen i avsnitt 2.

1.3. Aukrust-modellens resultater

Anta nå at lønnssatsen settes slik at avkastningskravet i avsnitt 2 innfris, og at realisert lønnskostnadsandel samtidig er lik den andelen partene i arbeidslivet oppfatter som normalandelen. I dette tilfellet blir som nevnt lønnsfastsettelse basert på Aukrust-modellen identisk med lønnsfastsettelse basert på et eksplisitt avkastningskrav. Men er resultatene og antagelsene i Aukrust-modellen forenlig med resultatene i en slik løsning? Dette avsnittet belyser om resultatene i Aukrust-modellen er forenlige med resultatene man får i en slik løsning når man innfører produktivitetsvekst og prisvekst.

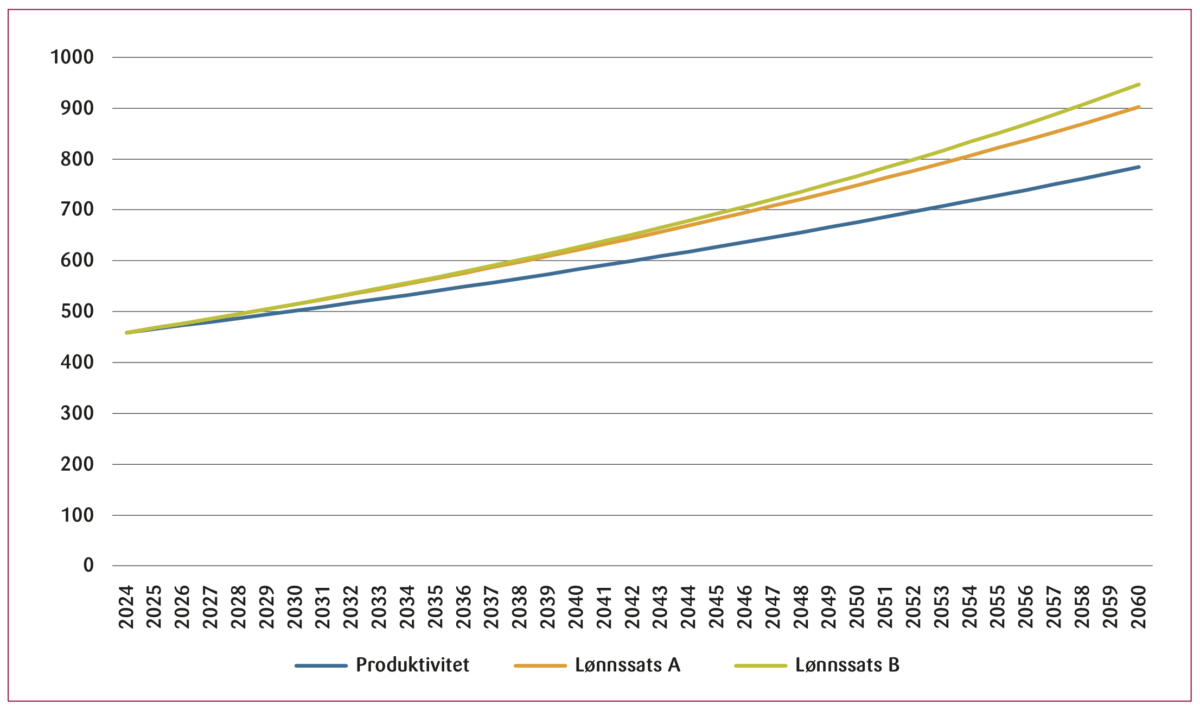
Aukrust-modellen impliserer at lønnssatsen i k-sektor må vokse i takt med produktiviteten i k-sektor når produktprisen holdes konstant. Modellsimuleringene viser imidlertid at lønnssatsen vokser mer enn den totale faktorproduktiviteten. Forklaringen er at produktivitetsveksten øker verdiskapningen, og dermed faktorinntekten. Avlønning av faktorene, arbeid og kapital, må derfor øke. En økning i avlønningen av begge faktorene tilsvarende produktivitetsveksten ville vært innenfor mulighetsområdet. Avkastningen per kapitalenhet er imidlertid uendret, så avlønningen til kapitaleierne er uendret. En prosentvis økning i lønnssatsen som tilsvarer økningen i produktivitetsveksten vil derfor ikke være tilstrekkelig. Lønnsveksten må være kraftigere enn produktivitetsveksten når avlønning per kapitalenhet ikke endres, se Figur 1. Modellsimuleringene viser at denne effekten forsterkes hvis substitusjonselastisiteten mellom kapital og arbeidskraft økes. I scenario B, med en substitusjonselastisitet på 1,66, vokser lønnssatsen raskere enn lønnssatsen i Scenario A, med en substitusjonselastisitet lik 0,85. Det er altså feil at lønnsveksten i k-sektor må være lik produktivitetsveksten når produktprisen i k-sektor holdes konstant.

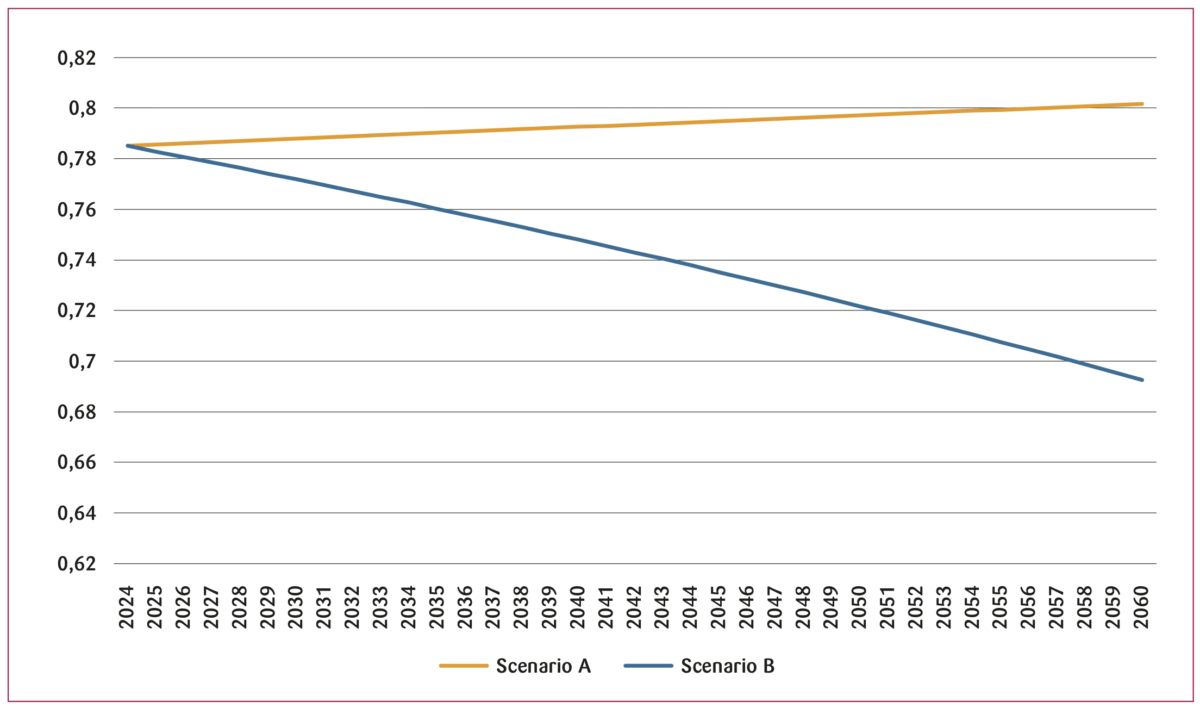
I Aukrust (1977) antas det at lønnskostnadsandelen er konstant over tid. Modellsimuleringer viser imidlertid at utviklingen i lønnskostnadsandelen bestemmes av nivået på substitusjonselastisiteten. Antar man at substitusjonselastisiteten mellom arbeidskraft og kapital er (tilnærmet) lik 1, blir lønnskostnadsandelen ikke påvirket av produktivitetsvekst som fører til vekst i lønnssatsen i kombinasjon med et uendret kapitalavkastningskrav. Antar man en substitusjonselastisitet lik 0,85, som i Scenario A, vil lønnskostnadsandelen vokse som følge av vekst i lønnssatsen i kombinasjon med uendret kapitalavkastningskrav. Forklaringen er som beskrevet ovenfor at veksten i lønnssatsen trekker lønnskostnadsandel opp, og at denne effekten dominerer. Dermed vokser lønnskostnadsandelen som følge av veksten i lønnssatsen, se Figur 2. Antar man derimot en substitusjonselastisitet lik 1,66, som i scenario B, vil lønnskostnadsandelen falle som følge av vekst i lønnssatsen i kombinasjon med et uendret kapitalavkastningskrav, se Figur 2. Forklaringen er at høyere lønnssats gir insentiver til å substituere arbeidskraft med kapital, noe som isolert sett reduserer lønnskostnadsandelen. Denne effekten dominerer i scenario B. Dermed faller lønnskostnadsandelen som følge av veksten i lønnssatsen. Antagelsen i Aukrust-modellen om at en konstant lønnskostnadsandel vil realisere en normal avkastning på investeringer i k-sektor er altså feil i dette tilfellet. Fagforeningenes fokus på å få en gitt del av kaka (verdiskapingen) kan dermed føre til lønnsvekst som reduserer kapitalavkastningen. Ovenfor påvises det at en slik lønnsvekst ville redusere lønnskostnadsandelen når substitusjonselastisiteten er større enn 1. Dermed forsterkes kravet om lønnsvekst. Dette fører igjen til en lønns- og lønnskostnadsandelsspiral som innebærer at investeringer i k-sektor blir ulønnsomme, noe hovedkursteorien skulle forhindre.

Hvis man isteden antar at den teknologiske utviklingen utelukkende er arbeidskraftforbedrende blir lønnskostnadsandelen konstant og uavhengig av substitusjonselastisiteten mellom kapital og arbeidskraft. Acemoglu (2003) gir en teoretisk begrunnelse for slik teknologisk utvikling. Nordhaus (1973) hevder imidlertid at denne formen for teknologisk utvikling mangler forankring i virkeligheten. En vesentlig del av den teknologiske utviklingen er innebygd i ny realkapital, som f.eks. nye avanserte traktorer og gravemaskiner. Det er denne nye realkapitalen i kombinasjon med arbeidskraft som øker produksjonsmulighetene. Andre typer teknologi, som roboter og AI, forventes som nevnt å erstatte arbeidskraft. Disse eksemplene viser at det kan være utfordrende å knytte den teknologiske utviklingen til spesifikke innsatsfaktorer.

I de senere årene har verdien på den norske krona svekket seg, samtidig som priser på varer i k-sektor har økt. Ifølge Aukrust-modellen vil prisvekst i k-sektor slå ut i en tilsvarende lønnsvekst på lang sikt. En slik prisvekst kan oppstå som følge av en varig svekket valutakurs. Analyse i denne artikkelen antar at prisen på varen som produseres i k-sektor er identisk med prisen på investeringsvarer. En økning i produktprisen i k-sektor øker verdiskapingen i k-sektor. Avkastningskravet per investert realkapitalenhet øker tilsvarende som følge av prisøkningen på investeringsvarer. Dermed øker driftsresultatet per kapitalenhet på tross av et uendret avkastningskrav per krone investert, altså uten at investorer har blitt mer grådige. Modellsimuleringer viser at lønnssatsen øker like mye som avkastningskravet. Siden faktorprisene øker like mye, forblir faktorforholdet uendret. Lønnskostnadsandelen forblir dermed også uendret. Siden arbeidskraften i k-sektor er uendret, blir også realkapitalmengde og produksjonen uendret. Prisveksten får altså ingen realøkonomisk effekt i dette tilfelle. Disse resultatene er forenlig med resultatet i Aukrust-modellen om at en prisvekst i k-sektor slå ut i en tilsvarende lønnsvekst på lang sikt.

4. KONKLUSJON

Hovedkursteorien i Aukrust (1977) inneholder hovedretningslinjene for hvordan lønningene bør fastsettes i Norge. Beskrivelsen av lønnstilpasningen på lang sikt er imidlertid mangelfull. Investorers avkastningskrav inngår ikke eksplisitt i bestemmelsen av lønnsnivået i Aukrust-modellen. Partene i arbeidslivet legger som omtalt i innledningen til grunn at en stabil lønnsandel indikerer at lønnsomheten er stabil. Men er dette premisset relevant i tiden framover?

Denne artikkelen tar utgangspunkt i Aukrust-modellens beskrivelse av lønnsfastsettelsen i Norge på lang sikt, der k-sektor er lønnsledende. Antagelsen om at normal avkastning på kapital sikres av en antagelse om konstante faktorinntektsandeler erstattes av et eksplisitt avkastningskrav basert på optimerende investoratferd. Artikkelen viser at et slikt avkastningskrav i kombinasjon med fri tilpasning av kapitalen er helt sentralt for tilpasningen av lønnsnivået på lang sikt. Artikkelen finner også at en lønnsfastsettelse som styrer mot en konstant lønnskostnadsandel på lang sikt, slik hovedkursteorien praktiseres, i empirisk relevante tilfeller vil føre til en lønns- og lønnskostnadsandelsspiral som gjør investeringer i k-sektor ulønnsomme. En slik lønnsfastsettelse vil være destabiliserende og skadelig for norsk økonomi. Utfallet kan imidlertid unngås ved at partene i arbeidslivet legger til grunn at en stabil fordeling av kaka ikke nødvendigvis innebærer stabil lønnsomhet i k-sektor. Artikkelen finner også at det er feil at lønnssatsen må vokse i takt med total faktorproduktivitet i k-sektor når produktprisen holdes konstant, slik Aukrust-modellen impliserer. Lønnssatsen må vokse raskere enn produktiviteten, og lønnskostnadsandelen er ikke nødvendigvis konstant over tid.

Fotnoter:

1. En stor takk til Redaktør Rune Jansen Hagen og den anonyme konsulenten,
   Ådne Cappelen, Erling Holmøy, Håvard Hungnes, Birger
   Strøm og Thomas Von Brasch for nyttige kommentarer. ↩︎
2. I denne konteksten er det rimelig å tolke «normal avkastning» som et
   avkastningsnivå som innfrir investorers avkastningskrav. ↩︎
3. De siste tiårene har lønnskostnadsandelen i mange vestlige land falt.
   Karabarbounis og Neiman (2014) finner at utviklingen forklares av
   lavere priser på investeringsvarer i kombinasjon med en substitusjonselastisitet
   mellom arbeid og kapital som er større enn 1, mens Kheng
   mfl. (2024) finner at økt eksport og mindre usikkerhet forklarer utviklingen.
   Flere ledende økonomer hevder imidlertid at utviklingen skyldes
   en forskyvning i makt fra arbeidstakere til kapitaleiere. Bjørnstad
   mfl. (2016) finner støtte for denne hypotesen, samt at substitusjonselastisitet
   er lik 1. ↩︎
4. Lønnsfastsettelsen i de makroøkonomiske modellene KVARTS og
   NORA er modellert som forhandlingsløsninger mellom partene i arbeidslivet.
   Løsningene er empirisk forankret i arbeidsmarkedsstatistikk,
   og sentrale elementer fra hovedkursteorien inngår i løsningene.
   Eksplisitte kapitalavkastningskrav er imidlertid ikke inkorporert i selve
   lønnsfastsettelsen i disse modellene. Merk at lønnskostnadsandelen i
   industrien anslås til 0,72 i nye reviderte nasjonalregnskapstall for 2024,
   mens gjennomsnittet for de siste tiårene var rett under 0,8. ↩︎